在群里扔过这样一个问题。当时我也不知道怎么回答：

Delta对冲组合Theta是10000，当前的IV是32。第二天开盘跳开3个点，行情没再动直接收盘，IV没动，问组合当天的盈亏是多少钱？

刚开始完全无从下手。想着算盈亏，必然跟期权组合的PnL公式有关。 \[ \Delta PnL=\delta \Delta S + \frac{1}{2}\Gamma (\Delta S)^2 + \theta\Delta t + \nu \Delta \sigma\] 其中\(\delta\)已对冲，IV没动所以\(\Delta \sigma =0\)。重点考察中间两项，

\[\Gamma=\frac{N^{'}(d_1)}{S \sigma \sqrt{T}}\]
\[\theta=-\frac{S_0 N^{'}(d_1)\sigma}{2\sqrt{T}}-rKe^{-rT}N(d_2)\] 因为\(r\)和\(N(d_2)\)很小，近似忽略\(\theta\)后半部分。将\(\Gamma\)换成\(\theta\)的表达式并化简， \[\Delta PnL=\theta\Delta t [1-\frac{(\Delta S/S)^2}{\sigma^2 \Delta t}]\] 这也就解决了上面提出的问题。唯一需要注意的细节就是一年按365，还是按252或者256来算。

回答完问题之后，再回过头来想想。其实题目和\(\Delta PnL\)最终的形式，是在告诉我们\(\Gamma\)收益和\(\theta\)收益是可以相互转化成波动率形式的。那不妨，用\(\Gamma\)来表示下损益： \[\Delta PnL=\frac{1}{2}\Gamma S^2 [(\frac{\Delta S}{S\sqrt{\Delta t}})^2-\sigma^2]\Delta t\] 如果说\(\Delta PnL\)可以理解为瞬时损益的话，那右边是个啥？

先来看\((\frac{\Delta S}{S\sqrt{\Delta t}})^2\)，可看作\(\Delta t\)时间内标的资产收益率的真实方差，如果从过去展望未来的话，就叫做RV。 \(\sigma^2\)恰是计算上述希腊字母时使用的收益率，一般使用IV，代表你price in的成本。

所以说，期权组合损益是跟未来实际波动率与对未来波动率预期之间差值成比例关系的。你可以选择组合做多或者做空波动率，即称作波动率交易。而要最大化这种收益，构造的组合自然是使得Gamma最大，所以也叫long Gamma或者Short Gamma策略，也就是买跨或者卖跨。尤其经典的是卖跨策略。

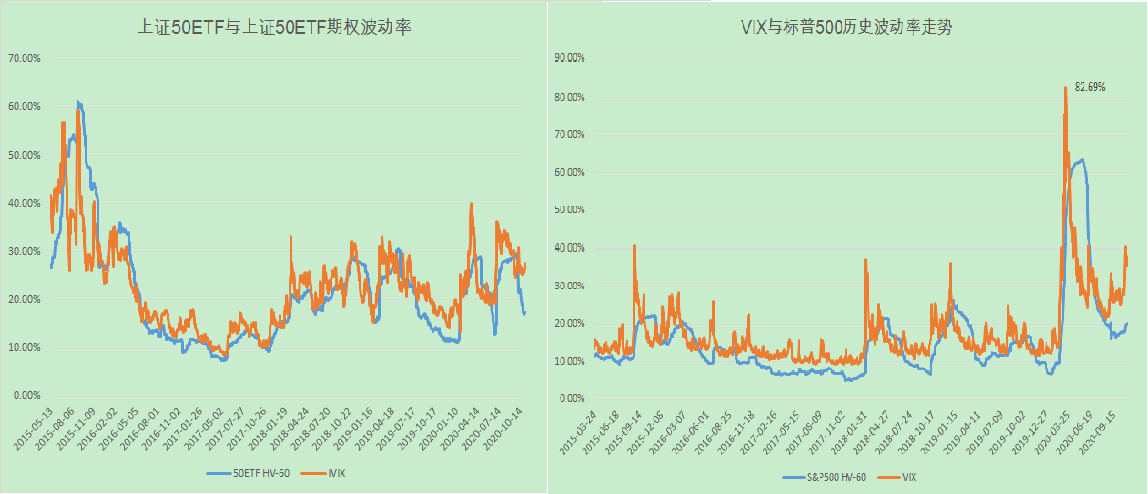
上面是让凤娟帮忙画的两幅图，可以看出无论是S&P500的VIX还是国内50ETF的IVIX指数，除剧烈波动期间，市场总是持续对波动率预期过高，反映在隐含波动率总是大于历史波动率。这才是short Gamma策略的内因。原因呢？比如杠杆成本，机构多头需要买保费等等，也不一定正确，大家可以多发散理解。

注意单单看这个图的Volatility Spread还不够，因为是要未来的RV大于现在的IV才能盈利。所以本质还是波动率的均值回归属性，在震荡期，特别是波动率下行期才是Short Gamma的好时机，不仅能赚真实波动率的钱，还能赚Vega的钱。

前面都是考虑瞬时损益，而总损益是对\(dt\)的积分： \[PnL=\int_{0}^{T}\frac{1}{2}\Gamma S^2 (RV^2-IV^2) dt\]

\[=\int_{0}^{T}\frac{1}{2}\Gamma S^2 (RV+IV)(RV-IV)] dt\] \[\approx \int_{0}^{T}\Gamma S^2\sigma(RV-IV)]\] 同时，Vega的表达形式为： \[\nu = S\sqrt{T}N^{'}(d_1)=\Gamma S^2 \sigma T\] 代入上式， \[PnL=\int_{0}^{T}\frac{\nu}{T}(RV-IV)dt\] \[=\nu(RV-IV)\] 即是Vega收益。同时，我们还有另外一个Vega收益，那最终的\(PnL\)： \[PnL=\nu(RV-IV_0)+\nu(IV_1-IV_0)\] 注意\(\nu\)、\(IV\)和\(RV\)是随着\(S\)和\(T\)变化的。综合下来，其实Theta、Gamma和Vega收益是不能割裂来看的。

另外几个点还有说一下：

• Short Gamma策略是负Gamma，所以Gamma端始终是亏钱的，这是因为在对冲Delta时永远在高买低卖。
  
• 侥幸一下，不对冲行不行（也即留下敞口，能否带来投机收益）？不行，Delta敞口暴露永远是在亏钱的，而且亏钱的速度越来越快，对冲好Delta敞口是第一要义。
  
• 除了策略收益，还需要考虑摩擦成本，对冲不及时成本，交易费用等等。

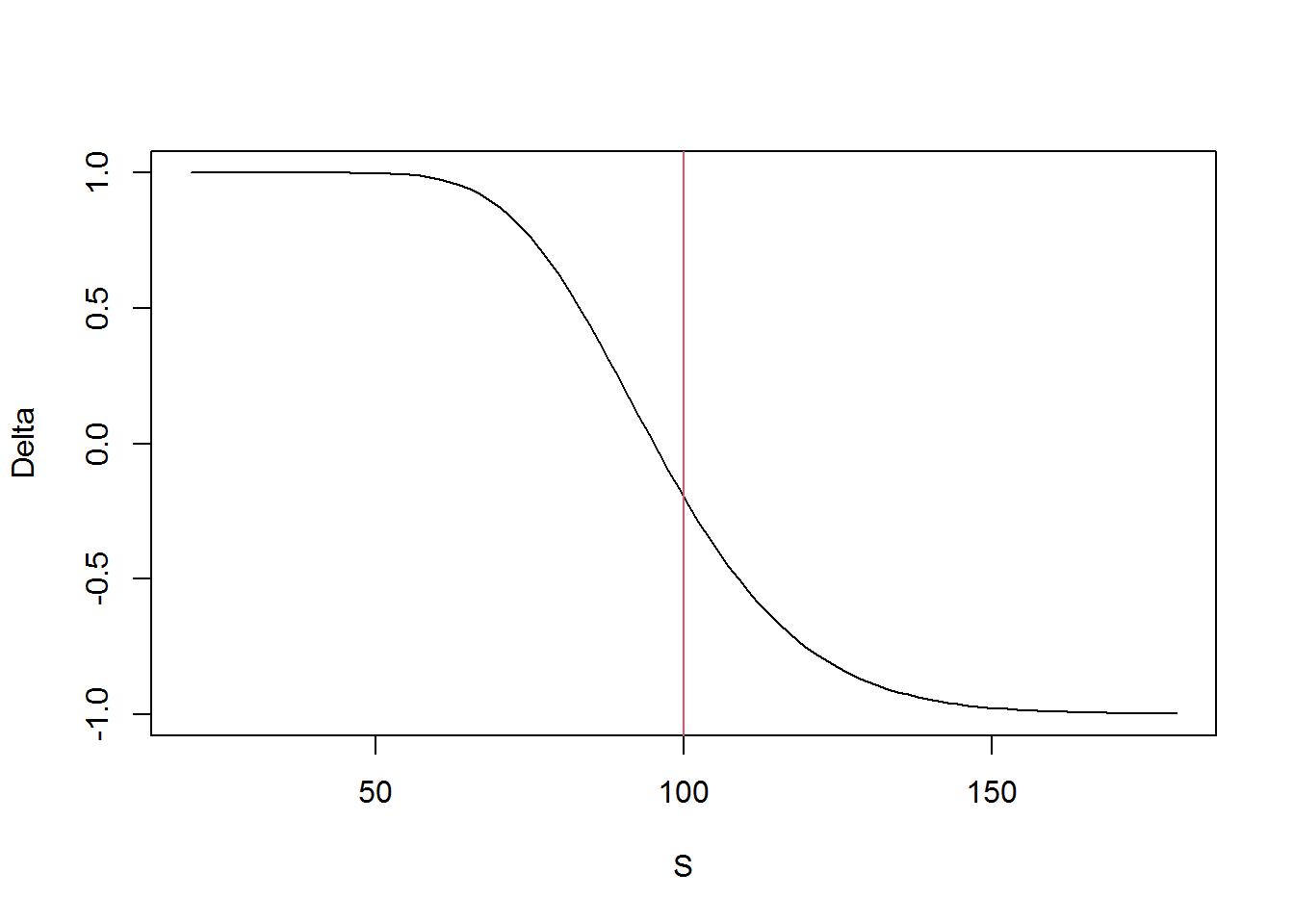
用图来解释下第1点和第2点。Short Gamma策略的Delta是\(1-2N(d_1)\)，与\(S\)的关系是：

接下来还有个重要的问题：

不同的对冲规则或者对冲条件，对损益或者风险影响有多少？比如风控指标里面的Delta比例80-125，再比如瞄准当天损益、标的资产涨跌幅等等来对冲，差别有多大？这些难以通过公式来表达的，可以通过蒙特卡洛生成10000条路径的方法来解决。