Option Margin Analysis
cq / 2020-11-30
这篇短文,主要理解期权保证金公式,以及研究下保证金风险度变化规律,方便盯市。
1. 定义
交易所ETF期权公式定义:
看涨期权 \[c+max\{12\% S-max\{K-S,\quad 0\},\quad 7\%S \}\] 看跌期权 \[min\{p+max\{12\% S-max\{S-K,\quad 0\},\quad 7\%K \}, \quad K\}\]
虽然公式看起来很复杂,其实是按合约不同的虚实状态来计算的,覆盖2交易日的波动。从图形上来看更明显:
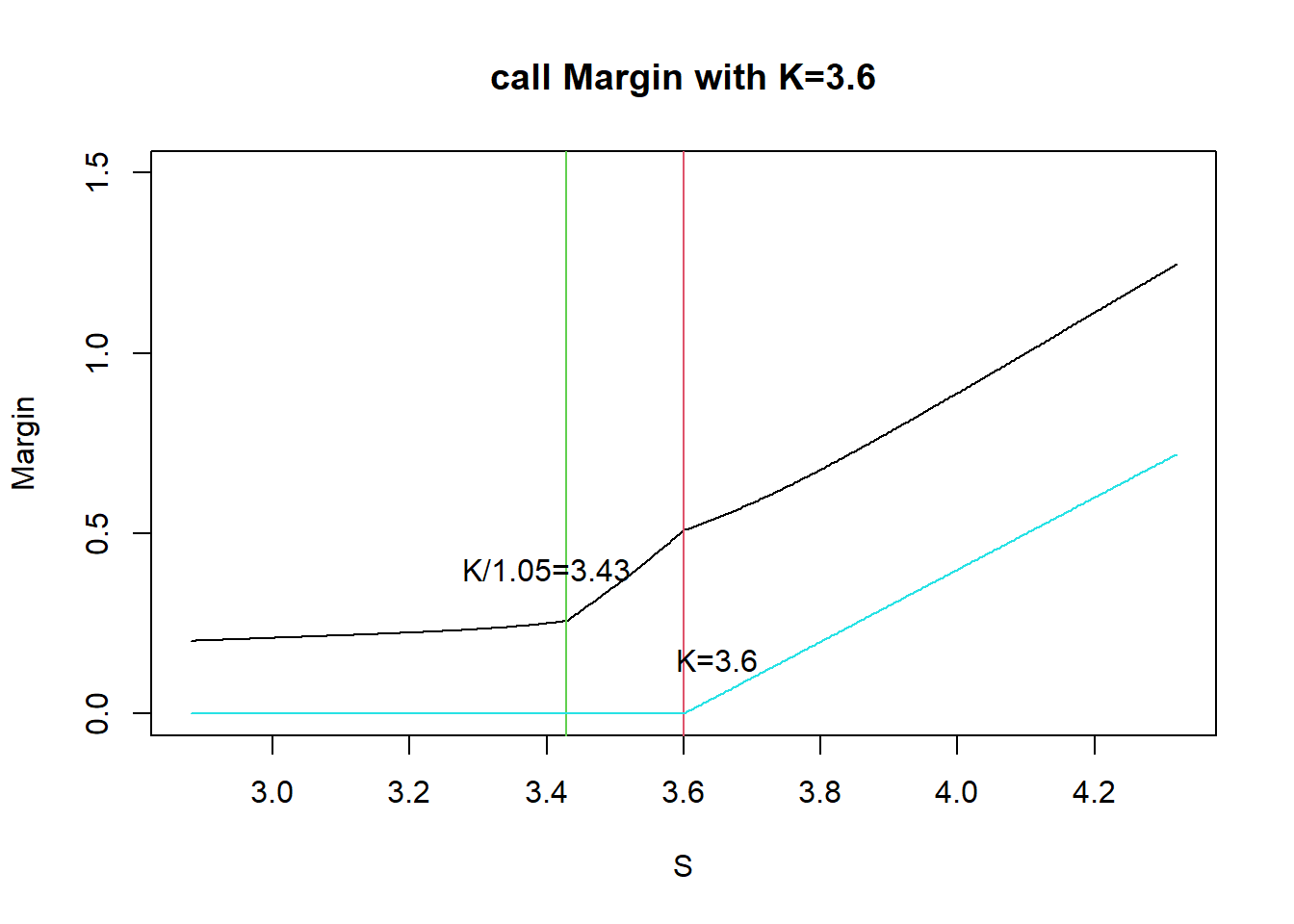
大抵可以看出斜率分三个阶段:
- \(S<\frac{K}{1.05}\),深度虚值状态:Margin=\((0.07+\delta)S\)
- \(\frac{K}{1.05}<S<K\),浅度虚值状态:Margin=\((1.12+\delta)S-K\)
- \(S>K\),实值状态:\((0.12+\delta)S\)
\(delta\)也在逐步变大。在转向实值阶段,收取保证金的速度最大,保证金比率变化最快。
看跌期权类似
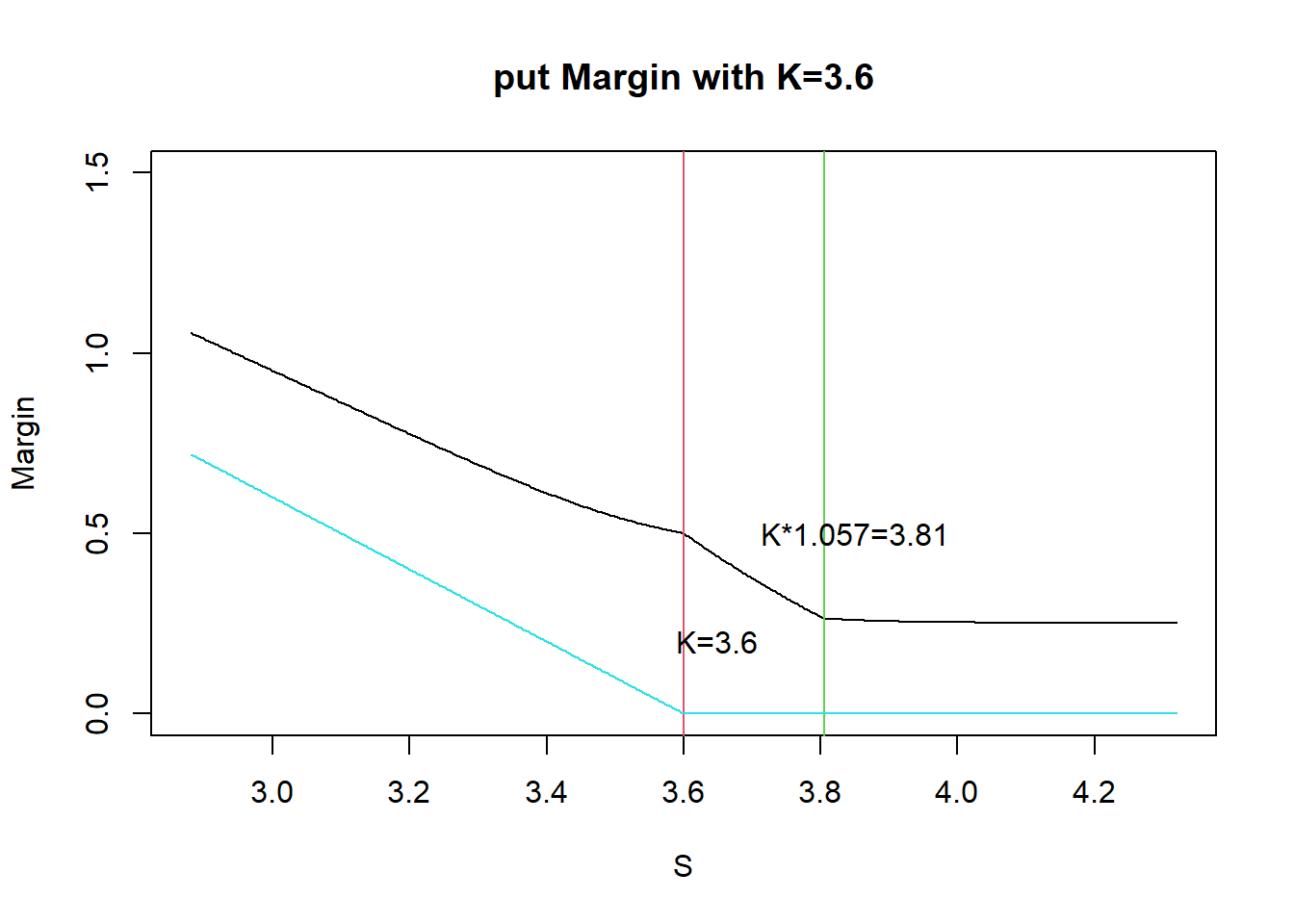
卖跨呢?
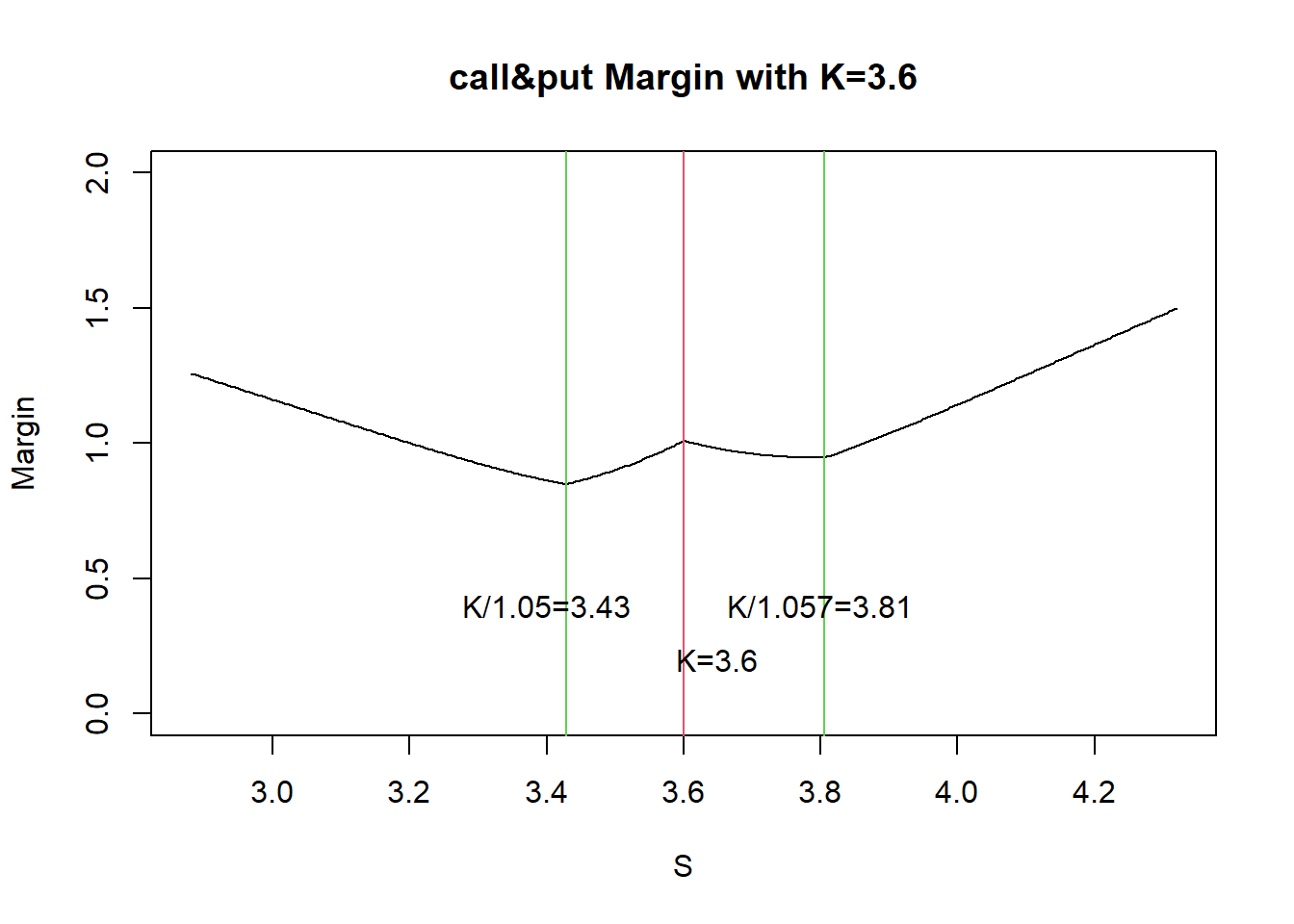
卖跨在平值时占用较高,但往往是在平值处开仓,留有一定保证金空间。所以卖跨更关心行情大幅波动(\(\pm5\%\))后的保证金占用。
2. 保证金比率
对保证金风险度的影响更重要,因为可能会爆仓。所以关心的是,当标的价格波动0.1%时,保证金比率会变化多少。这对现实盯市实践有较大意义。
假设当日无操作,保证金账户余额不变, \(k_0\)为初始保证金风险度。
\[Initial \quad Margin \quad ratio =\frac{Margin}{Cash+Margin}=k_0\]
当S上涨幅度为r时,计算call的保证金风险率\(k\)变动:
\(S<\frac{K}{1.05}\),深度虚值状态 \[M_0=(0.07+\delta_0)S\] \[\Delta k=\frac{(0.07+\delta)(1+r)S - (0.07+\delta_0)S}{M_0/k_0}\] \[=k_0\frac{0.07*r+(1+r)\delta-\delta_0}{0.07+\delta_0}\]
\(\frac{K}{1.05}<S<K\),浅度虚值状态 \[M_0=(1.12+\delta)S-K\] \[\Delta k=k_0\frac{[1.12*r+(1+r)\delta-\delta_0]S}{(1.12+\delta_0)S-K}\] 此阶段\(\Delta k\)公式是直接跟S和K相关的,但是关系大吗?应该还好,S和K偏离不超过5%,\(\Delta k\)取倒数可以观察出来。
\(S>K\),实值状态:
\[M_0=(0.12+\delta_0)S\]
\[\Delta k=k_0\frac{0.12*r+(1+r)\delta-\delta_0}{0.12+\delta_0}\]
结合图来看一下,涉图期权参数为:\(call: \quad \sigma=17.6\%,t=1/12,r=3\%,K=3.6\)
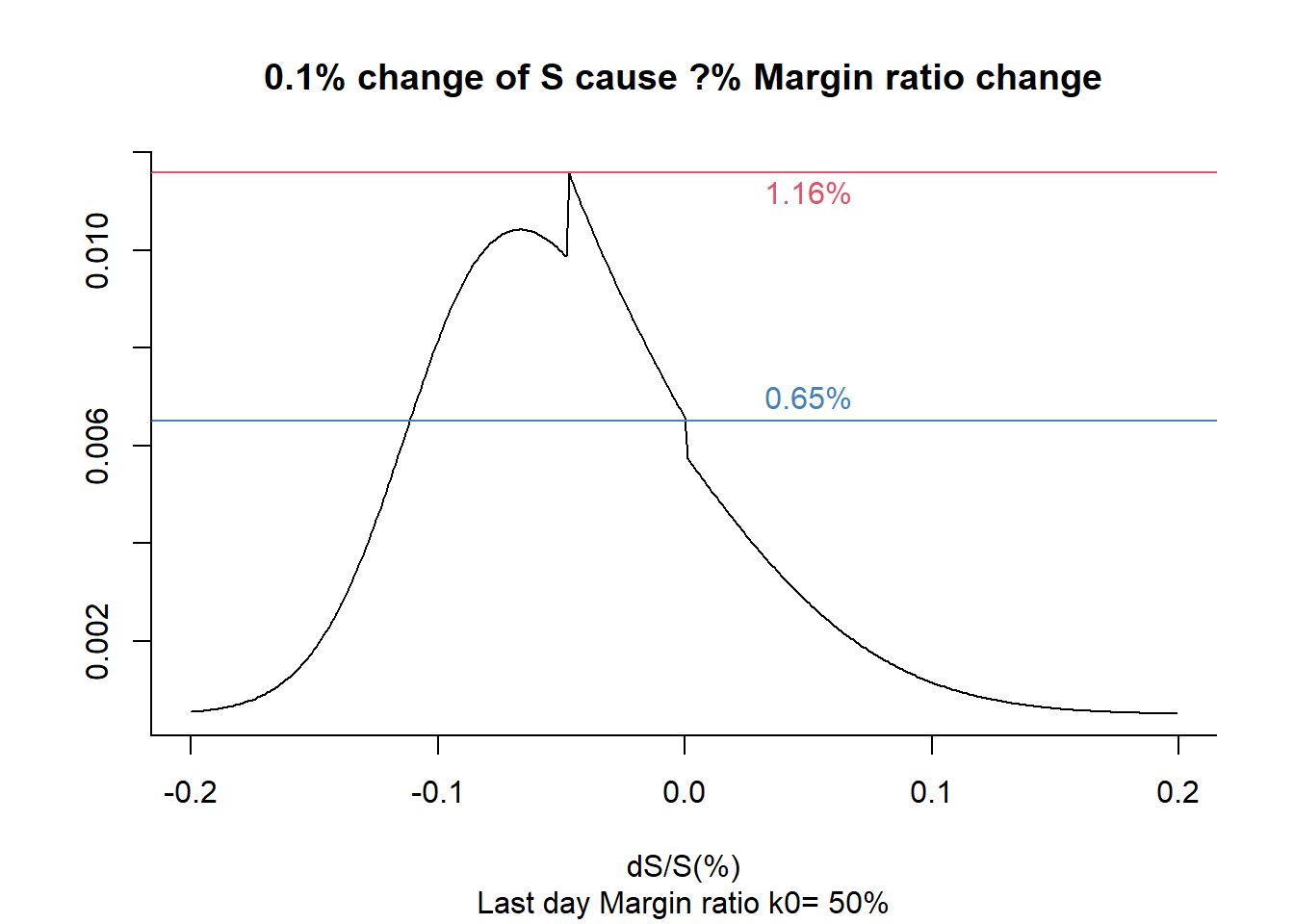
上图给出了当S波动0.1%时,在不同阶段保证金的变化幅度。很有意思的是,抛开接近实值凸起阶段,上面那么复杂公式给出的曲线竟然很像正态分布,期权真的很神奇。
从模拟情况来看,如果前一天收盘保证金比率为50%,S波动0.1%:
- 第二天在深度虚值和实值阶段,保证金风险度增加不超过0.65%;
- 但如果第二天处在虚值(距离执行价10%)向实值转变阶段,保证金风险度变动幅度从0.65%快速增加,在(距离执行价5%)阶段达到峰值,0.1%S变动,会导致1.16%保证金比例变动,这个速度是相对快了。如果初始保证金大于50%,那速度就更快了。
- 在S偏离(小于)执行价3%-8%,保证金比率10倍于现货波动很容易发生。
上文给出的峰值1.16%,是依赖于产品波动率(\(\sigma=20\%\))和到期时间(\(t=1/12\))的。
3. 波动率与到期时间的影响
我们定义在初始保证金比率为50%时,S波动0.1%时,保证金比率波动最大值(Maximum Margin Ratio Change, MMRC).
\[MMRC(\sigma,t)\quad and \quad MMRC(20\%,1/12)=1.16\%\] 看看两者影响程度如何?
3.1 波动率的影响
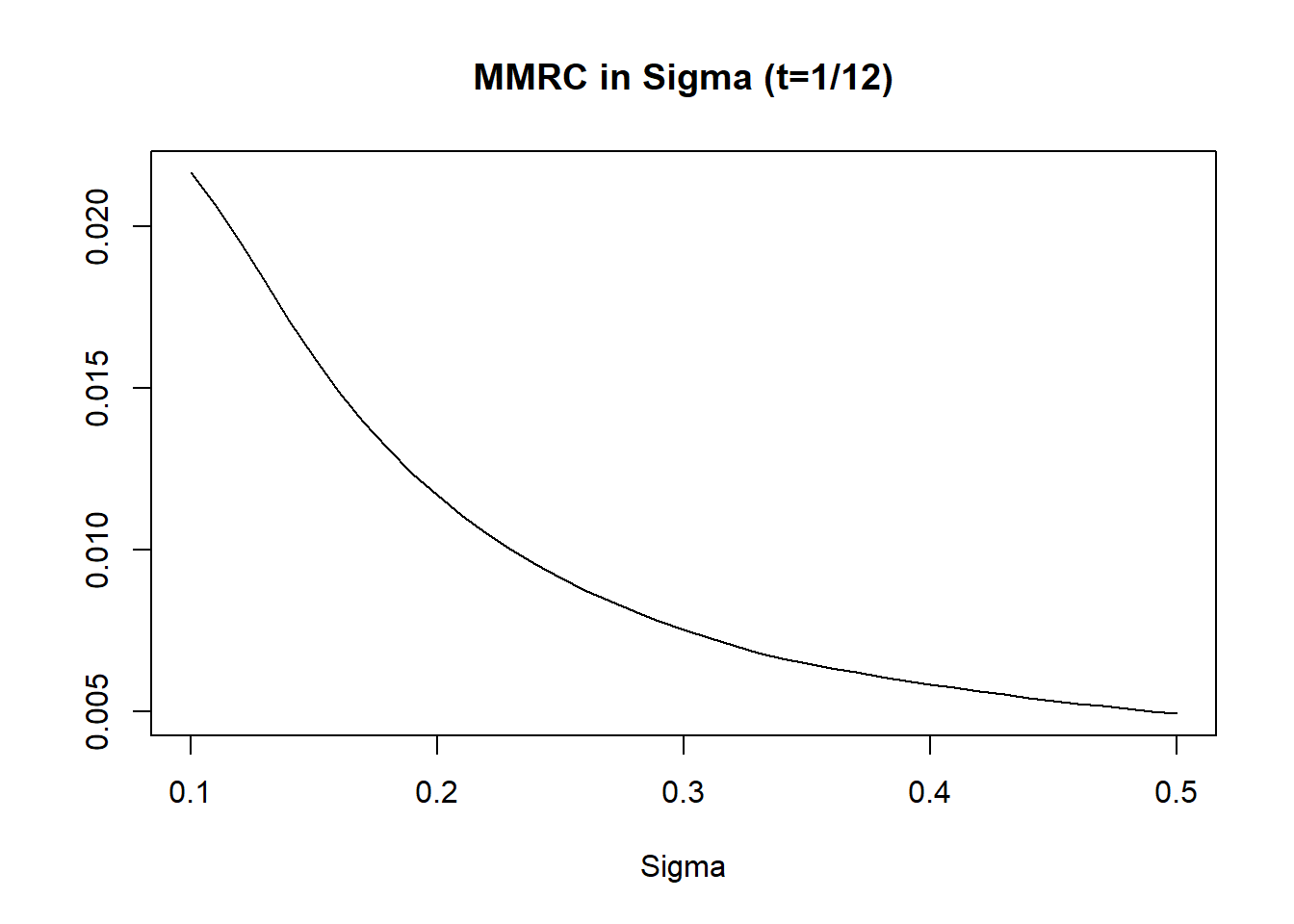
波动率越小的市场环境,保证金占用变少,\(\delta\)变陡了,\(\delta\)变化值变大了,所以MMRC也变大了。波动率15%时,MMRC是20%时的一倍左右。
这是一个需要关注的点,波动率越小,小幅震荡,无聊行情时,越容易松懈和想当然。但此时保证金风险度变化 非常敏感,在S偏离(小于)执行价3%-8%这段范围内,波动率在15%(这个波动率水平不稀奇),1%的现货波动会引起15%左右的保证金比率变化。
回过头来,保证金在小幅震荡的环境下少收点,但是比率变化更敏感,这样设计是科学的,这是个很好的风控指标设计理念。
3.2 到期时间的影响
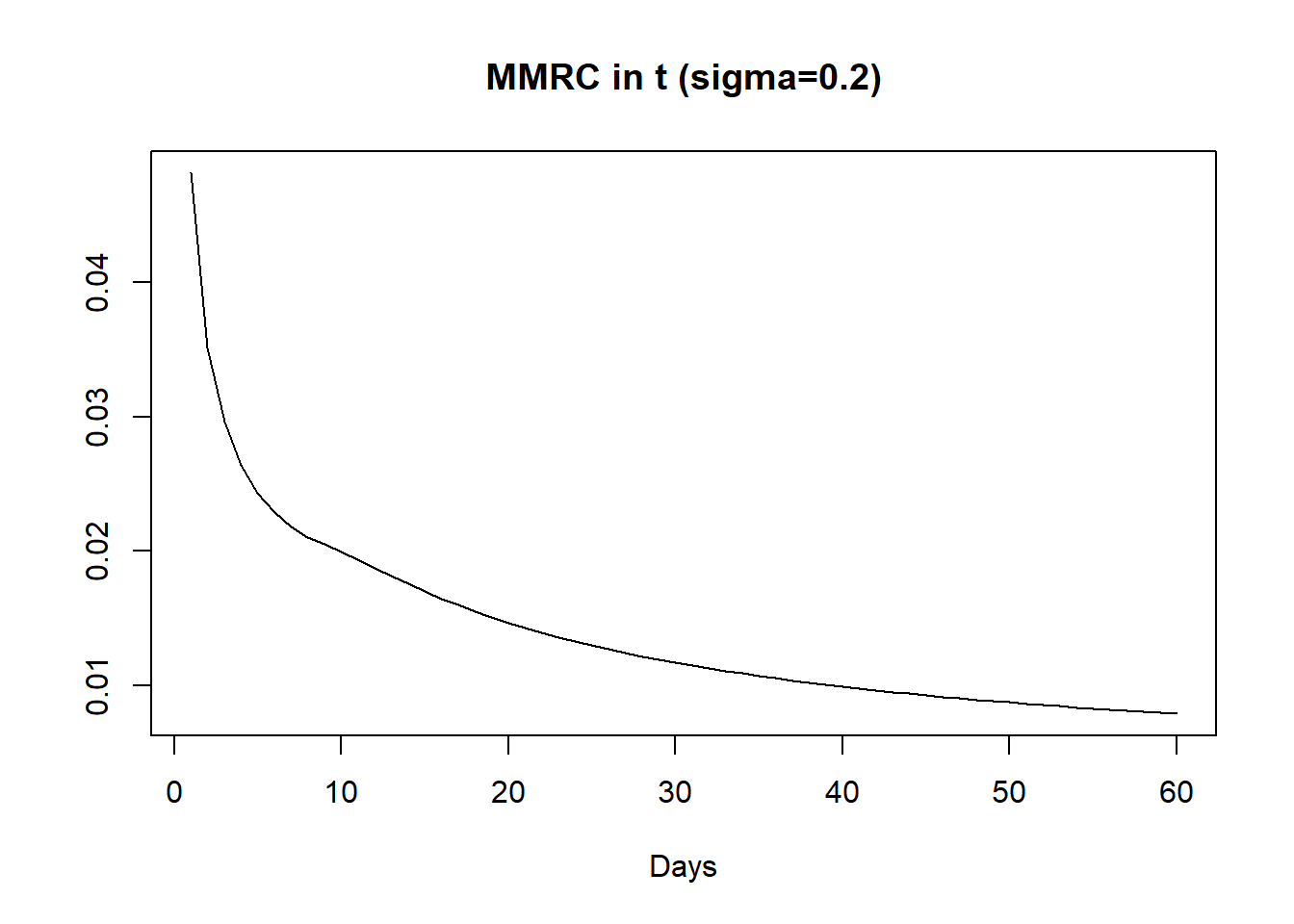
到期时间跟波动率对MMRC的影响方式一样,只是后者更敏感。
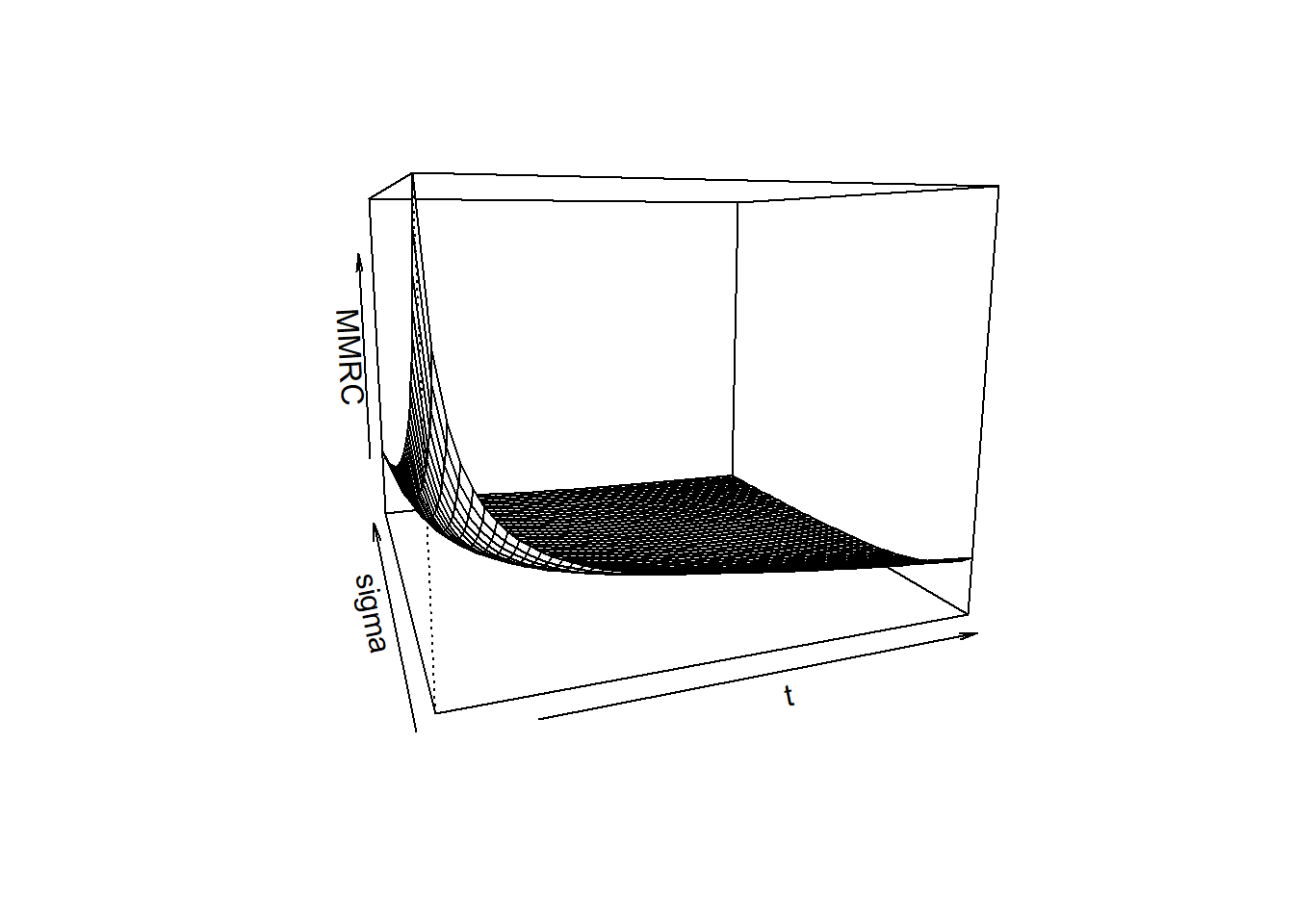
三维图没啥特殊凸起区域,可不予关注。
以上结论,应该是具有普适性,供参考。