分红与衍生品
cq / 2020-12-10
股票作为权益性资产,是可以参与分红的。而衍生品作为一项义务或者权利合约,本身不参与分红。因此分红事件会对衍生品定价产生影响。当然这种影响可以通过制度设计予以规避。
1. 标的分红
股票分红相对清楚,在公告日\(T_0\)知悉,将在\(T\)日对标的资产除息,并于若干日后支付红利\(D\)。如无其他因素影响, \[ S^{开盘}_{T}=S^{收盘}_{T-1}-D \] 每只股票分红都会反应在价格里,影响市值,从而每次分红都会影响股票价格指数,特别是大权重股。而ETF基金,则对当年所有分红累积,集中一次作利润分配,也即ETF分红,比如2020年11月11日,上证50公告每份分红0.051,并于同月30日除息。
2. 对期货的影响
期货通过构建无风险套利组合来定价的。分红期在\(T\)内,
| 时间 | \(T_0=0\) | \(T_1\) | \(T_2\) | …… | \(T\) |
|---|---|---|---|---|---|
| 交易1 | 借\(S_0\)现金,买入现货并持有 | 分红\(D_1\) | 分红\(D_2\) | 归还借款及利息\(S_0e^{rt}\) | |
| 交易2 | 以\(F_0\)价格空头进入期货合约 | 用持有的现券,以\(F_0\)价格了结合约 | |||
| 净现金流 | 0 | \(D_1\) | \(D_2\) | \(F_0-S_0e^{rT}\) |
按无风险套利原则, \[ F_0=S_0e^{rT}-D_1e^{r(T-T_1)}-D_2e^{r(T-T_2)} \\ =(S_0-D_1e^{-rT_1}-D_2e^{-rT_2})e^{rT} \]
如果基差 \(b=S-F\),没有分红的,理论基差 \(b=S(1-e^{rT})\);
有分红,理论基差 \[ b=S(1-e^{rT})+D_1 e^{r(T-T_1)}+D_2 e^{r(T-T_2)} \]
可以看出,分红如果在期货到期之前,是会影响期货定价以及基差的。像国内上市公司,分红期一般集中在5、6、7和8月份(上证50一般在后三个月)。如果你在4月份,观察当季和下季合约升贴水幅度,就是假的,是包含红利影响的。如果你不知道这回事,按假的贴水幅度,做跨期套利交易和风险管理,那是会吃亏的。
那如何计算刨除红利影响的真实升贴水幅度呢(大佬教的):
- 自己估计红利。用Wind取出成分股和权重,3年平均股利支付率和券商一致预测净利润,算出分红总额,按权重推算对指数的影响;
- 用指数期权来估计,但是目前只支持沪深300指数(下文会论及)。
3. 对期权的影响
如果资产分红,持有现货可以享受红利,而期权则不会,现货价格下降还会使得行权距离更远了。红利是否影响期权定价,取决于制度设计中除息是否调整合约行权价。
指数期权
在中金所上市的沪深300指数期权,未对分红作专门的制度设计。每只股票分红,按权重影响指数,指数从而影响期权。同样的,如果分红在期权合约期限内,期权定价就需要考虑分红的影响。
- 常规的,可预期的分红:市场会在合约上市时将分红因素定价在内;
- 突发的,临时的分红:期权价格会在红利公告日(不会等到除息日)反应意外分红的影响,价格会发生突变。
如何反应呢?因为分红属于无风险部分,将\(S_0-De^{-rT_1}\)作为新的标的资产初始价格带入BS公式计算分红影响的理论价格。
另外,按平价理论,
| 时间 | \(T_0=0\) | \(T_1\) | \(T\) |
|---|---|---|---|
| 组合1 | 买入看涨\(c\),现金\(De^{-rT_1}+Ke^{-rT}\) | \(S_T\ge K,S_T+De^{r(T-T_1)}\\S_T<K,K\) | |
| 组合2 | 买入看跌\(p\),持有现货\(S\) | 分红\(D\) | \(S_T\ge K,S_T+De^{r(T-t)}\\S_T<K,K\) |
\(T_1\)除息调整,行权价不调整。在\(T\)时,组合1和组合2的价值一样,根据无风险套利原则: \[ c+Ke^{-rT}=p+S-De^{-rT_1} \] 那我们可以根据上式,推算出大概的\(D\),从而反过来去计算期货的真实升贴水度。当然你也可以反过来,但是期货的合约有限,不容易区分贴水和分红影响。
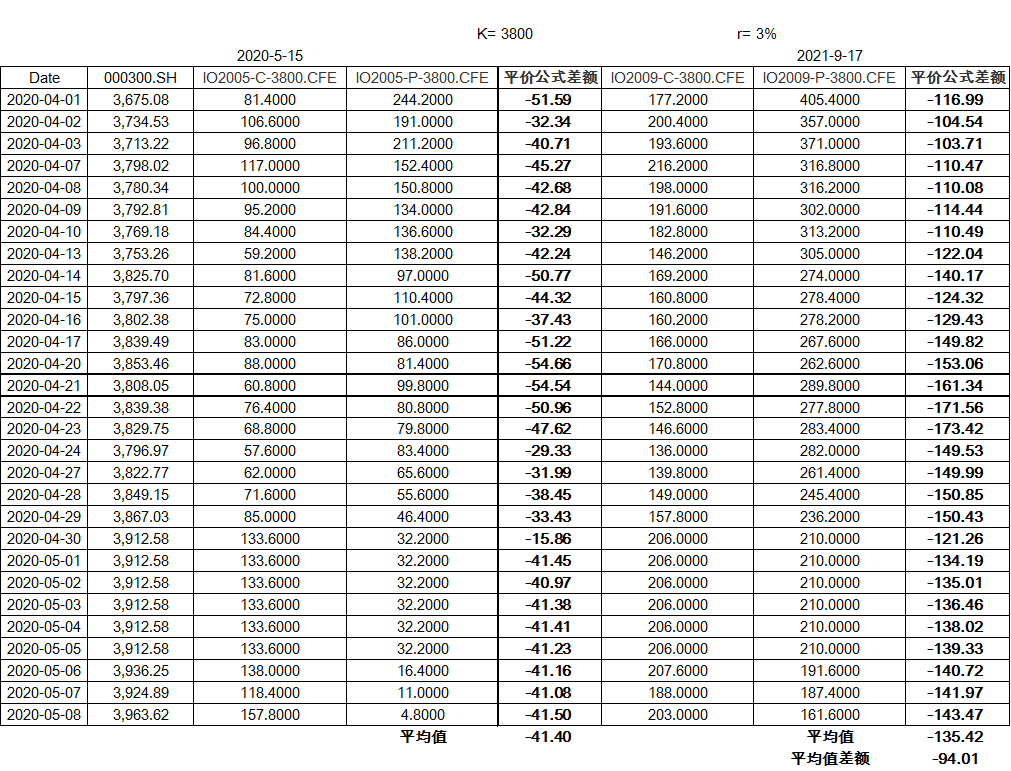
选择5月份(基本不受红利影响)和9月份(受大面积分红影响)在3800点位作为执行价的4份合约,按2020年4月以及5月初的期权行情数据,计算\(c+Ke^{-rT}-p-S\)求平均后作差值,估计沪深300指数在6、7、8以及9月到期前的分红点数为94点。
站在今天(2020年12月10日)来看,指数4940点,Wind统计股息率为2.09%,计算近12个月红利103点,估计的差不多。
ETF期权
ETF分红不同于指数分红,前者会集中当期分红作一次利润分配。比如沪市的300ETF,单位分红相对稳定,但是2019年分红时间整整提前1个月。如果像指数期权一样,让投资者自行预测分红幅度和时间。那当2019年12月5日分红公告后,4个到期日的合约价格都会突变反应分红因素的影响,深度虚值合约,都可能直接腰斩。散户一脸懵,又被割韭菜了,表示这玩意儿本来就复杂,还要自己算分红来定价??
为避免上述情况发生,沪深交易所ETF期权做了专门的制度设计,详见《上海证券交易所股票期权试点交易规则》。在除息日:
- \(S\)变为\(S-D\)造成行权距离变大,那就调整期权行权价格为\(K^*=K\times\frac{S-D}{S}\);
- 调整行权价格之后,期权理论价格会变为 \(c*=c\times \frac{S-D}{S}\)(不复杂,可按BS公式自行证明),所以调整除息日前结算价为\(c*\);
- 为保持期权合约市值(\(c\times M\))不变,那调整合约乘数\(M^*=M\times \frac{S}{S-D}\);
- 调完之后,重新挂牌原梯队行权价格合约。
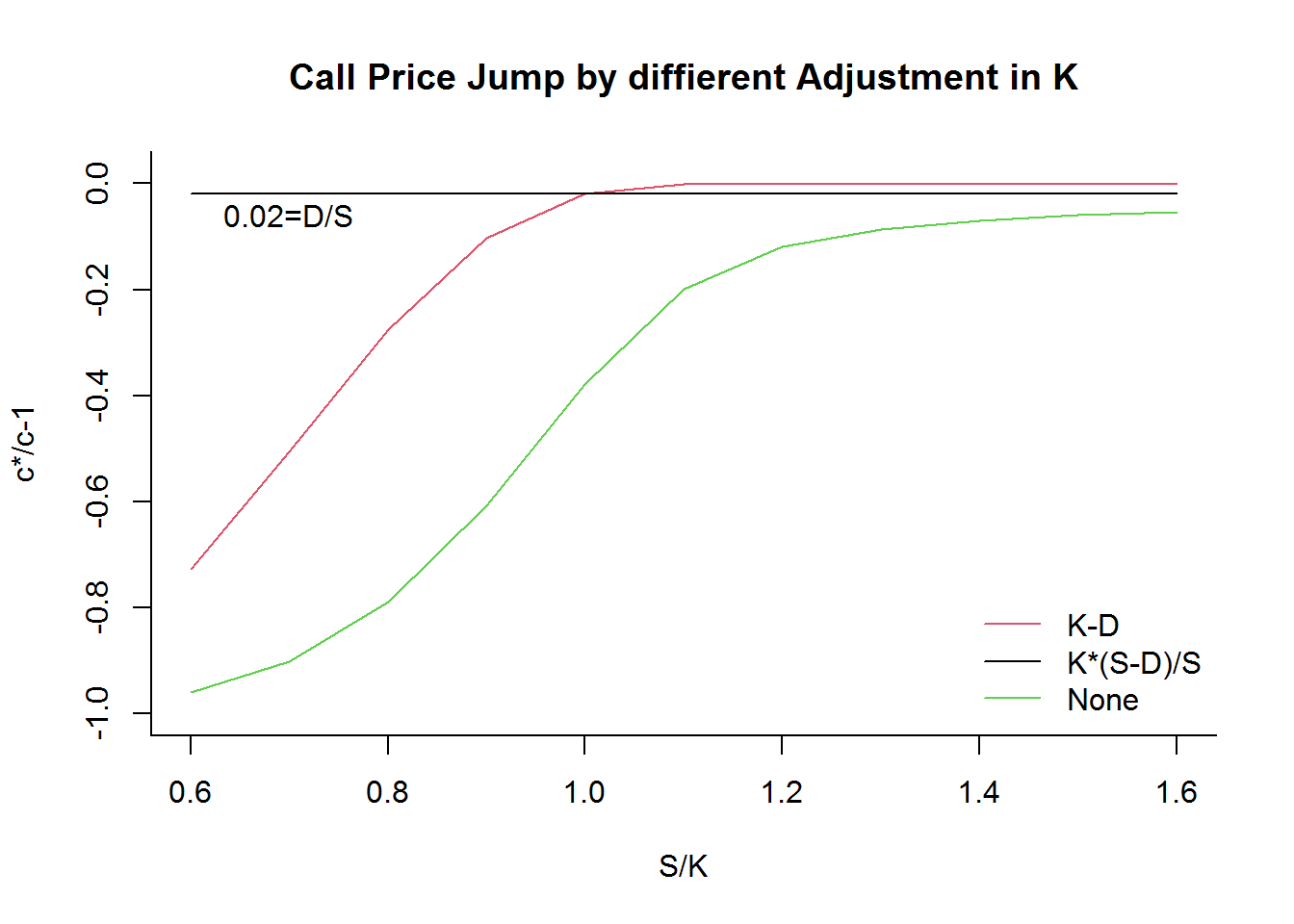
我开始比较好奇,为啥不\(K^*=K-D\) 呢? 因为这样设计,不能对深度虚值合约进行很好的调节,此类合约价格变化幅度仍然会很大。而设计\(K^*=K\times\frac{S-D}{S}\),期权价格变动百分比固定,即为股息率\(\frac{D}{S}\)。模拟结果如下,x轴为虚实程度,y轴为期权价格变动百分比。好的制度设计真的非常重要!
合约调整之后,备兑需要加锁现券;Delta对冲的话,单位合约 \(\delta\) 没变,但合约乘数变了,需要重新增加对冲(分红再投资就可以),其他希腊字母也需要重新对冲。
4. 最后
行文至此,关于分红对衍生品的影响,通过大佬指点以及自己摸索,大抵是搞明白了。涉及到的一些细节,如分红期的虚假贴水,应是投资和风险管理的基本专业要求。仅此记录。