关于bear和bull spread的几点记录
cq / 2021-07-11
主要回答以下几个问题:
- 此类垂直价差的盈利模式是怎样的?
- call spread和put spread 有区别吗?
- 基于当前现货位置,选择两个什么样的行权价?
一、盈利模式
call和put,bear和bull,总共4个组合。我们分别来inspect。约定\(S\)为现货价格,\(K_1\)和\(K_2\)是执行价,\(K_1<K_2\)。
1. bear spread
构建bear spread,也就是构建负delta的组合。
(1)call bear
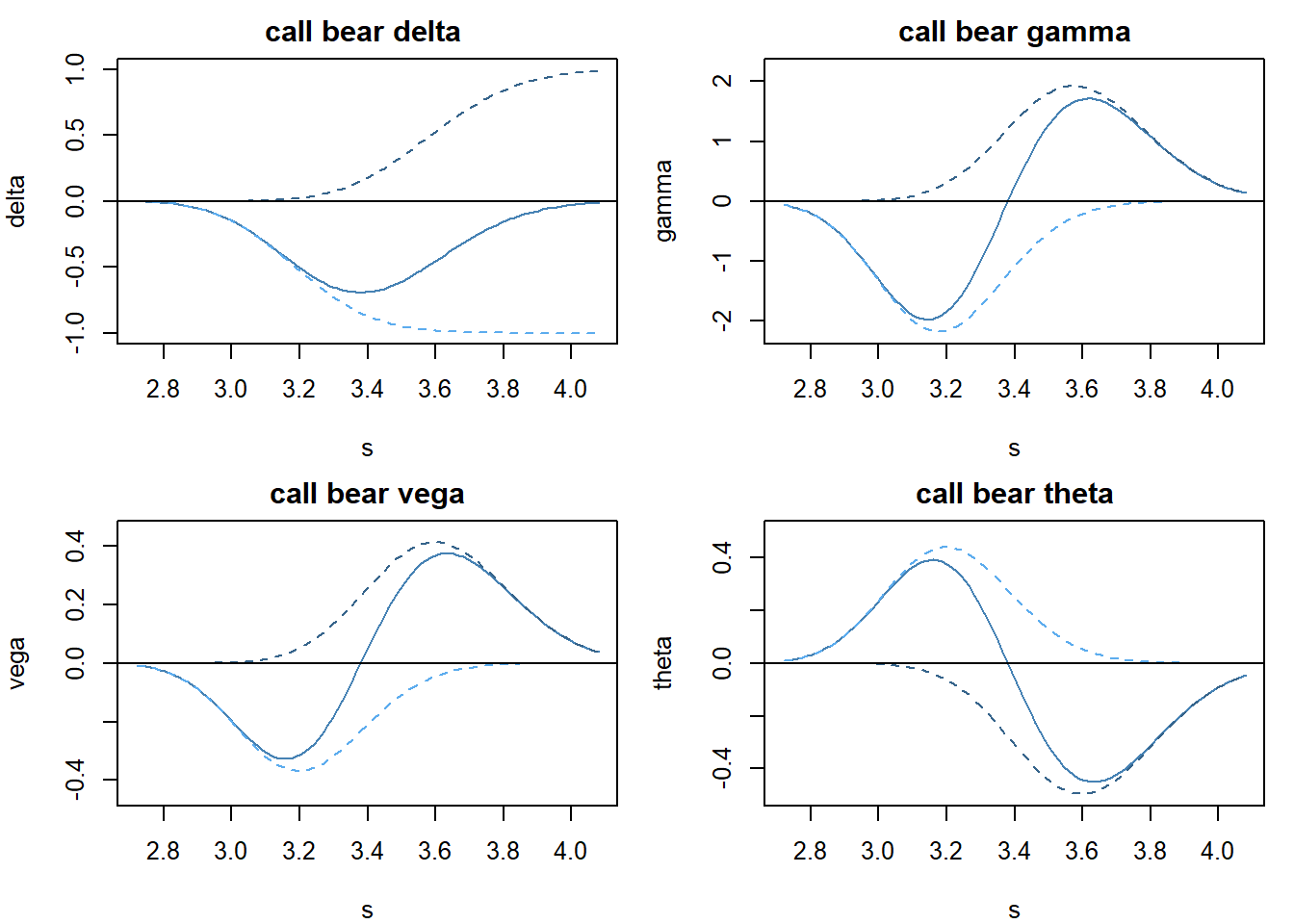
根据call 的delta 特征,short \(c_{1}\),long \(c_2\)。其中\(c_1\)是实值合约,所以call bear组合,建仓时是净现金流入的。
先看看组合的希腊字母(\(K_1=3.2\), \(K_2=3.6\)):
(2)put bear
除了delta,其实put就是call,call就是put。当需要构造负的delta的时候,那long \(p_2\), short \(p_1\),属于净现金流出。因为跟call bear都是在\(K_1\)执行价上short,在\(K_2\)执行价上long,所以gamma,vega和theta是相同的(前提是波动率接近)。而delta也是相同的,如下:
\[ \Delta_{p_2} - \Delta_{p_1}=N(d_{1}^{2})-1 - N(d_{1}^{1})+1 = N(d_{1}^{2}) - N(d_{1}^{1})=\Delta_{c_2} - \Delta_{c_1} \]
2. bull spread
其实就是 bear spread的头寸反过来,构建正delta的组合。
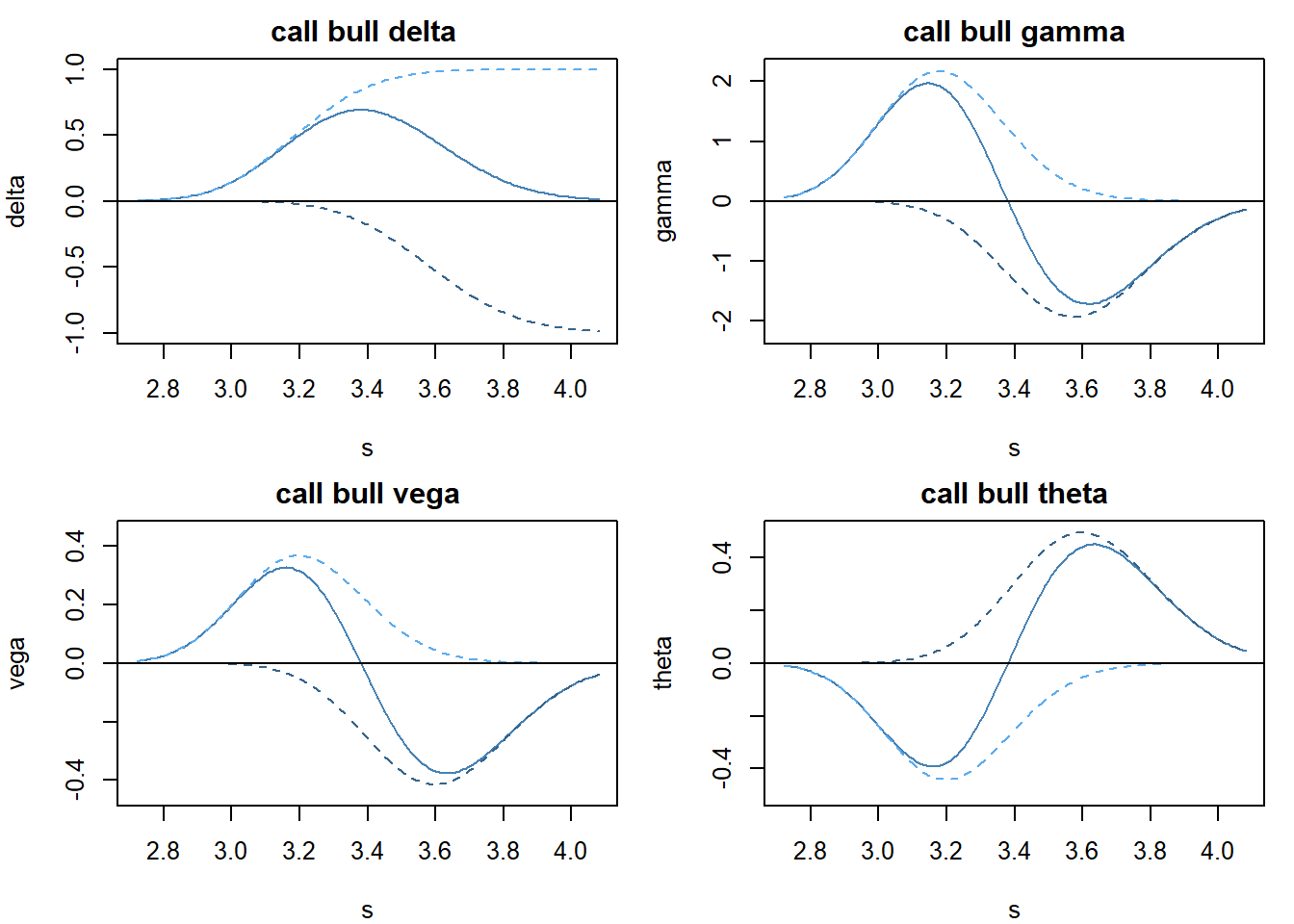
(1)call bull
long \(c_{1}\),short \(c_2\),建仓时是净现金流出的。希腊祖母,按x轴反转就可以了。同上\(K_1=3.2\), \(K_2=3.6\)。
(2)put bull
同put bear道理,不再赘述。唯一变化的是,这是一个净现金流入的组合。
3. 盈利模式总结
delta 大概在\(\frac{K_1+K_2}{2}\)的位置取得最大,如果现货价格在这附近起伏,这段时间组合的损益是delta起主要作用。
gamma会让delta绝对值在变小的过程中,经历一个慢快慢的过程。比如bear spread 在价格下降的时候,gamma会让我们赚没那么多了,当然价格上升的时候,也让我们不用亏那么多。
theta很重要,当价格下跌的时候,theta会转正,且在\(K_1\)位置取得最大值。这个下跌过程中,我们赚delta得钱,同时还赚theta的钱,并且theta逐渐起主要作用。但是如果方向反了,两个都在亏钱。所以做垂直价差,方向非常重要。组合建仓时,是现金流入还是现金流出,这个跟赚或者亏theta无关。
vega跟gamma类似,不过有意思的是,一般下跌的时候IV在上升,上涨的时候IV在下降,所以vega会帮助bull spread,欺负bear spread。当然这是经验法则,需要根据市场情况具体看,特别是市场缓慢变化的时候。
现货什么样的轨迹,才对策略最有利呢?其实根据希腊字母,最优应该是现货快速变动到期望的执行价上(熊小牛大)赚到delta的钱,然后在该执行价上停留足够久,赚取short端的时间价值,即theta的钱。盈利模式这一点适用于以上4个组合,跟其他东西无关。
我们用call bull(其他三个相同结果)模拟一下,三种现货的运动轨迹,快速上涨后稳住,逐步上涨和稳住不变后期快速上涨。
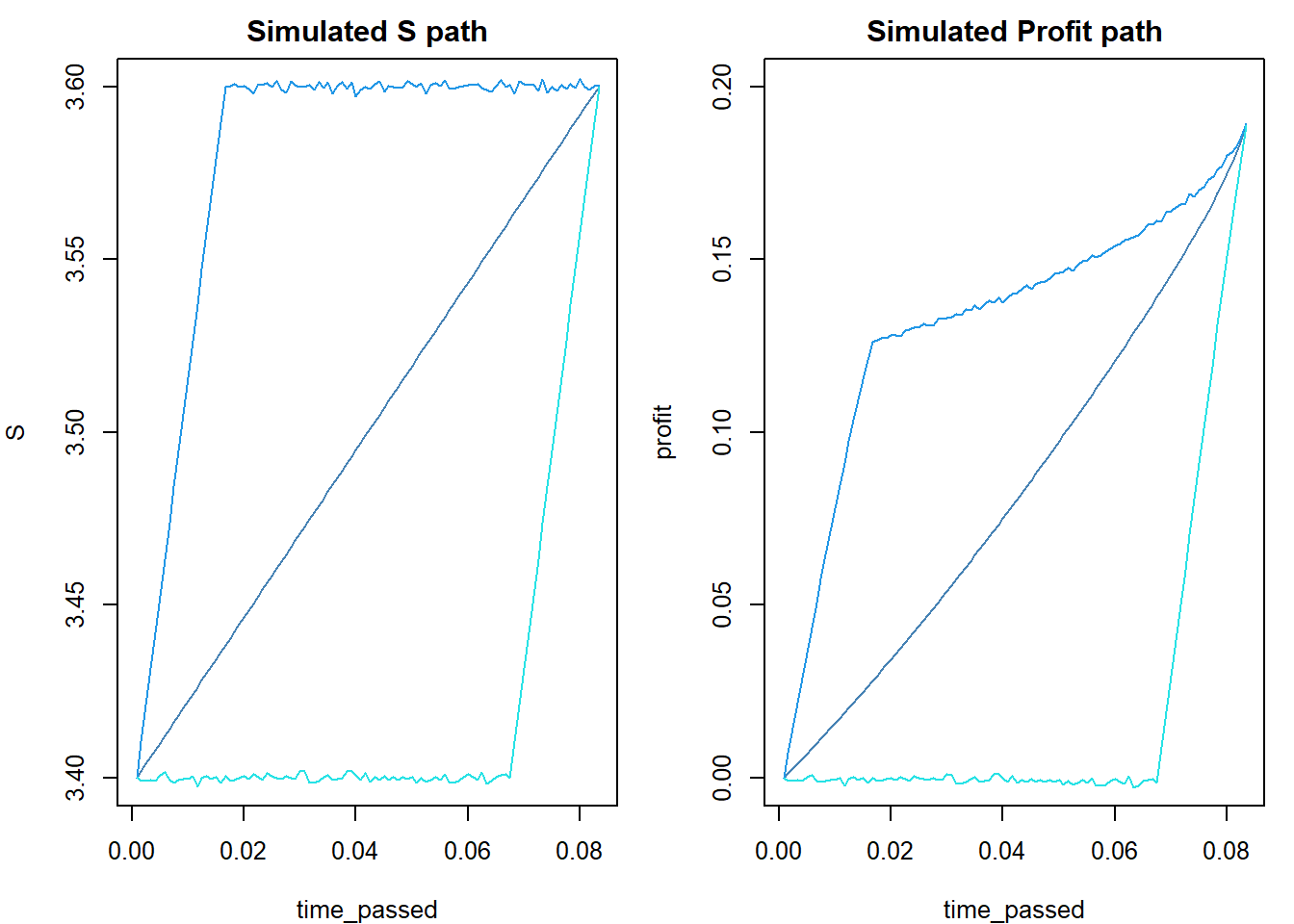
模拟结果佐证了上述加粗部分的结论。当然,多数时候是在赚完delta的钱后,就平仓了,这时候时间过去不久,资金效率更高。
二、call 和 put构造的spread有区别吗?
希腊字母和盈利模式方面,上面已经解释过了,两者完全相同,没有区别。我们从以下其他几个维度,进一步考虑:
- 会在什么时候,两者其一的价差会相对更有优势吗?应该不会,因为平价公式的存在,会使得两者价差之间相差\(K_2-K_1\),如果存在优势,也是不足以套利的微小优势。
- 波动率会导致区别吗? call端波动率与put端波动率水平差距明显,比如2021年7月1日那次,call端波动率极低,put端波动率略高。bear spread策略可以赚delta收益,但是如果用call bear,那vega上会亏钱,适合用put bear。分析思路就是组合的vega图。
- 会存在资金使用效率的区别吗?比如bear spread中,call bear属于净现金流入的,put bear属于净现金流出的。但是还需要考虑保证金占用的影响。call bear组合short实值的\(c_1\),会占用更多的保证金。put bear组合short虚值,占用更少的保证金,所有会有一个平衡。按交易所ETF期权保证金公式,具体来看一下:
实值\(c_1\)保证金占用,减去获取的期权费流入\(c_1-c_2\) \[ cash_{call}=c_1+0.12S-(c_1-c_2)=c_2+0.12S \]
虚值\(p_1\)同理: \[ cash_{put}=p_1+0.12S-S+K_1-(p_1-p_2)=p_2+0.12S+K_1-S \] 同时,根据平价公式,不考虑利息: \[ c_2+K_2=p_2+S \] 化简以下: \[ cash_{call}-cash_{put}=2*S-(K_1+K_2) \] 对于bear spread,期待S下降,用call bear占用保证金会比put bear少越来越多。同理,对于bull spread,期待S上浮,适合用put bear。
三、基于当前现货位置,选择两个什么样的行权价?
当对现货方向有大概判断之后,如何选择合约。至于选择call还是put来构造,上面部分已经解决了。现在解决具体选择什么样的\(K_1\)和\(K_2\)。有以下几点考虑:
\(K_1\)和\(K_2\)的区间需要多开。分得越开,delta抵消的越少,组合delta绝对值越大。而同时其他组合的希腊字母能维持中性。这本质上其实就是一个现货头寸了。分得越小,盈利空间也就越小了。除非特意构造现货头寸,一般按预判的涨跌幅(以及历史1个标准差的波动范围)来选择\(K_1\)和\(K_2\)的区间。
如何通过选择\(K_1\)和\(K_2\)来决定S和\(\frac{K_1+K_2}{2}\)的关系:
- bear spread:
- \(S\ge \frac{K_1+K_2}{2}\): delta会先增到最大,再减。所以delta收益会增厚;但是建仓初期,如果现货没有下探,theta每天都会带来损失;
- \(S< \frac{K_1+K_2}{2}\): delta收益会减薄,但是theta空间会大很多。特别是建仓初期,如果现货无波动,逐日仍然会有微小的theta收益。这点选择对心态很有帮助。当然这也是一个风险与收益之间的选择。
- bull spread:同上述,则优先选择组合\(K_1\)和\(K_2\)使得,\(S\ge \frac{K_1+K_2}{2}\)。
那么幅度多少呢?给个模拟结果供大家参考。在做bear spread时,哪怕选择\(K_1=S\),这时候theta基本最大,1天的theta收益也只能大概抗住+0.07%的现货涨幅带来的delta损失。
- bear spread: