cq

如何用Option对冲现货

cq / 2020-11-26

考虑采用期权对冲组合Beta，构造Alpha策略。先从指数ETF组合考虑起，因为就相差Alpha收益。

假设当前指数ETF价格为I，看跌期权价值为p，其中\(p=max\{K-I, 0\} + T\), T代表时间价值，可以小于0，但是不可能与\(K<I\)同时发生。

Part1 Delta对冲

先按Delta对冲，k为对冲系数，\(k=1/\Delta\), 同时\(\Delta\)是\(max\{K-I, 0\}\)的增函数。

1. 构建对冲价值变化

进入对冲时，组合价值为

\[P_t=I + k\times \{max(K-I, 0) + T\}\] 考虑期权到期,时间价值为0，经过\(\Delta t\), 组合价值 \[P_T=I+\Delta I + k\times max(K-I-\Delta I, 0)\]

价值变化量为 \[\Delta P=\Delta I + k\times \{max(K-I-\Delta I, 0) - \{max(K-I, 0) + T\}\}\]

2. 具体情况讨论

看起来很复杂，我们分情况讨论。

2.1 预测未来上涨

  1. 选择平值期权，K-I=0, \(\Delta=0.5\) \[\frac{\Delta P}{P}=\frac{\Delta I}{I}-\frac{2T}{I}\]

  2. 选择深度实值期权，\(\Delta=1\)

  1. 上涨幅度没有超过实值程度，\(\Delta I < (K-I)\) \[\frac{\Delta P}{P}= -\frac{T}{I}\]
  2. 上涨幅度超过实值程度，\(\Delta I > (K-I)\) \[\frac{\Delta P}{P}=\frac{\Delta I-(K-I)-T}{I}\] 如果选择深度实值合约，资金占用会较多(\(\frac{K-I+T}{I}\)),但时间价值会小于0,对冲层面到期始终会盈利。

2.2 预测未来下跌

  1. 选择平值期权，K-I=0, \(\Delta=0.5\) \[\frac{\Delta P}{P}=\frac{-\Delta I}{I}-\frac{2T}{I}\]

  2. 选择深度实值期权，\(\Delta=1\)

\[\frac{\Delta P}{P}= -\frac{T}{I}\]

3. 一般性模拟和结论

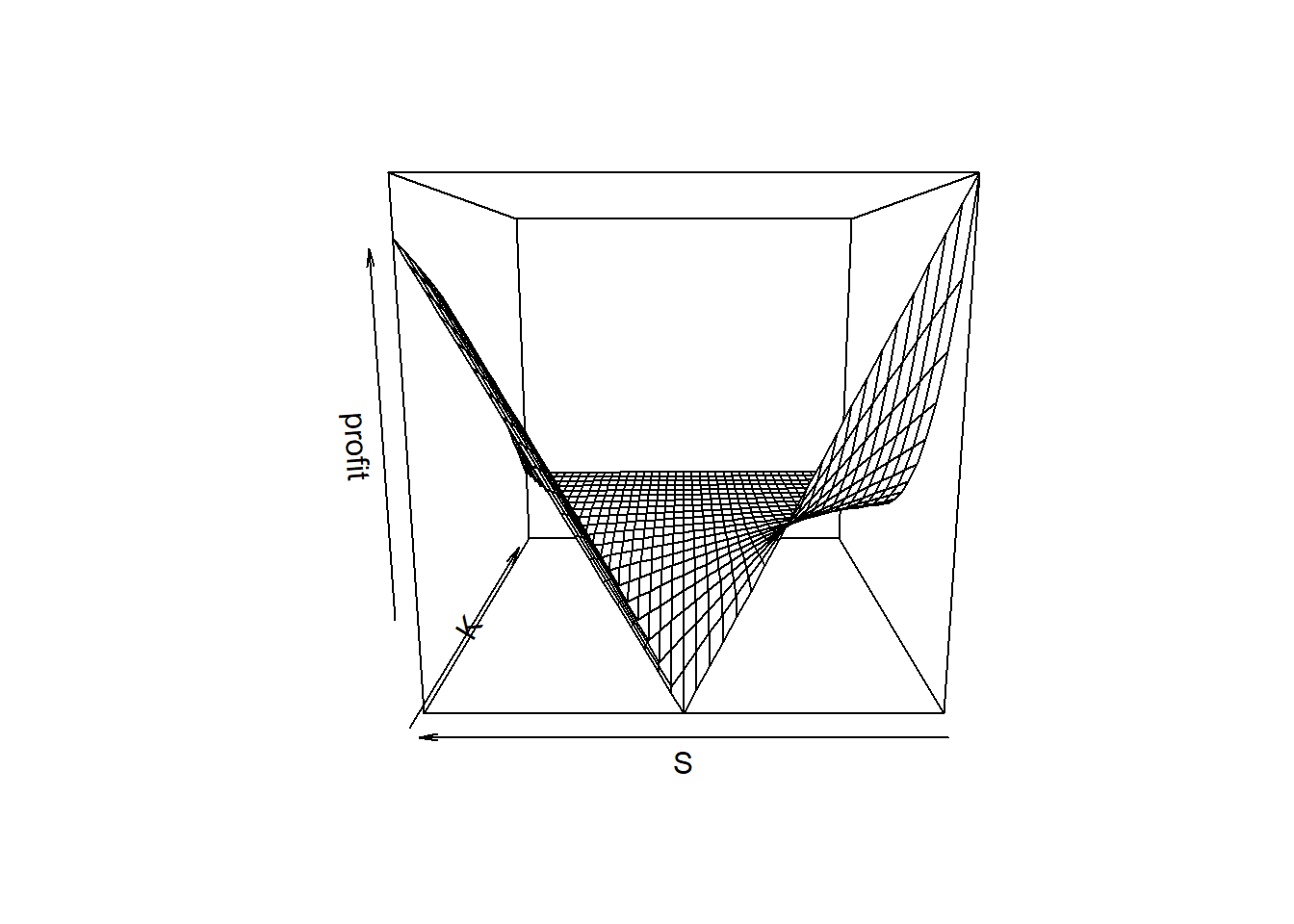
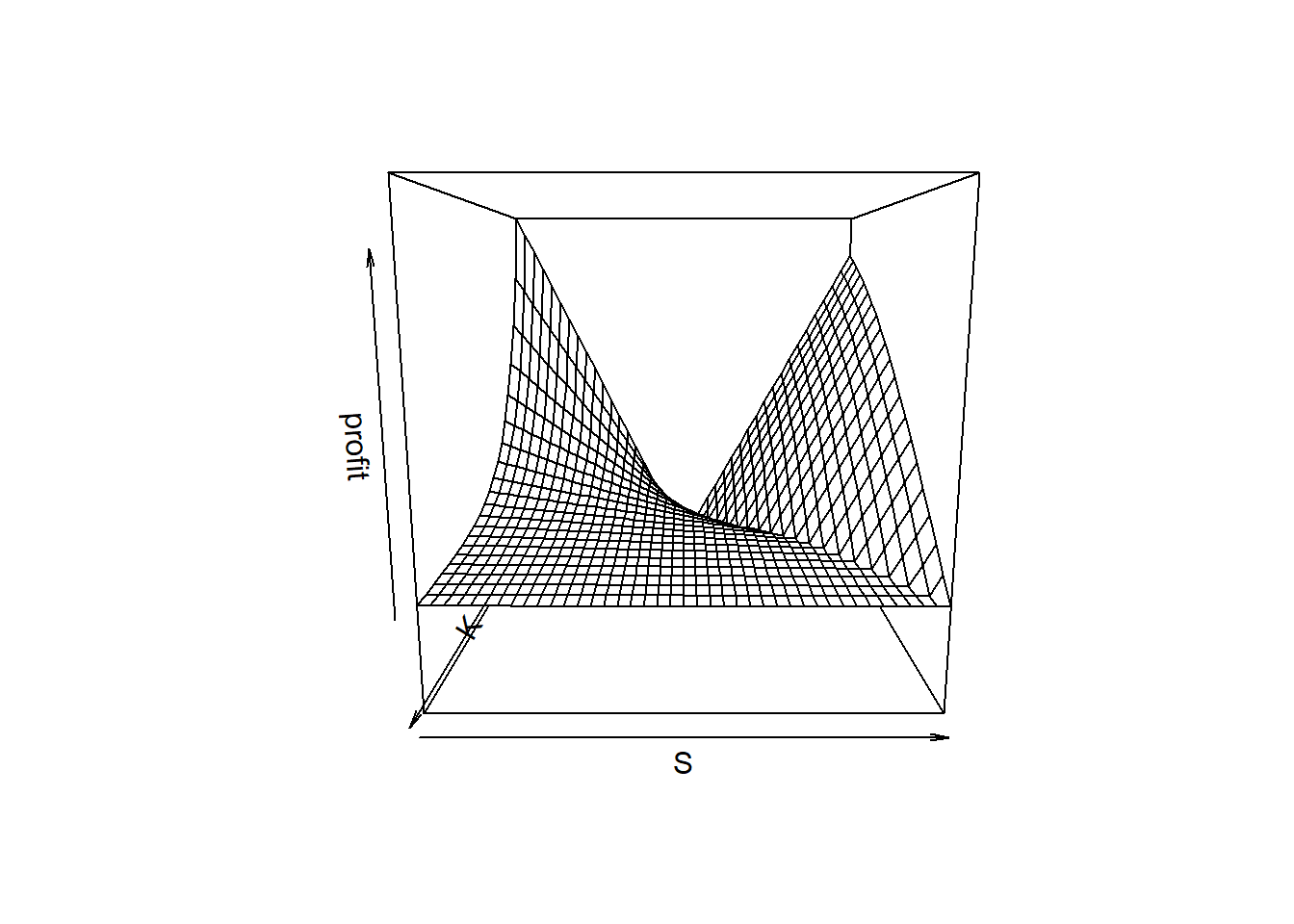
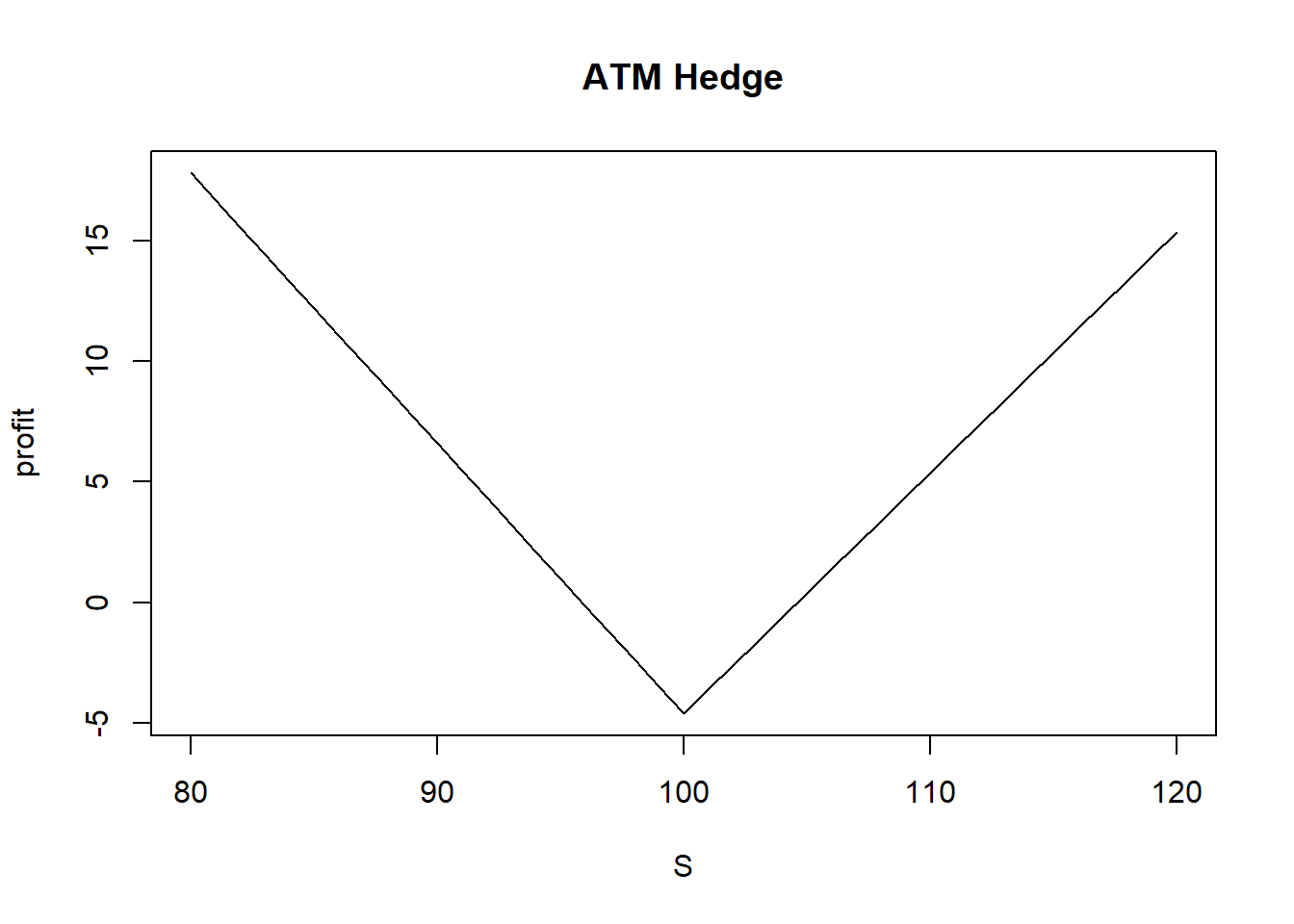
近4.5%的对冲成本，赚的回来吗？

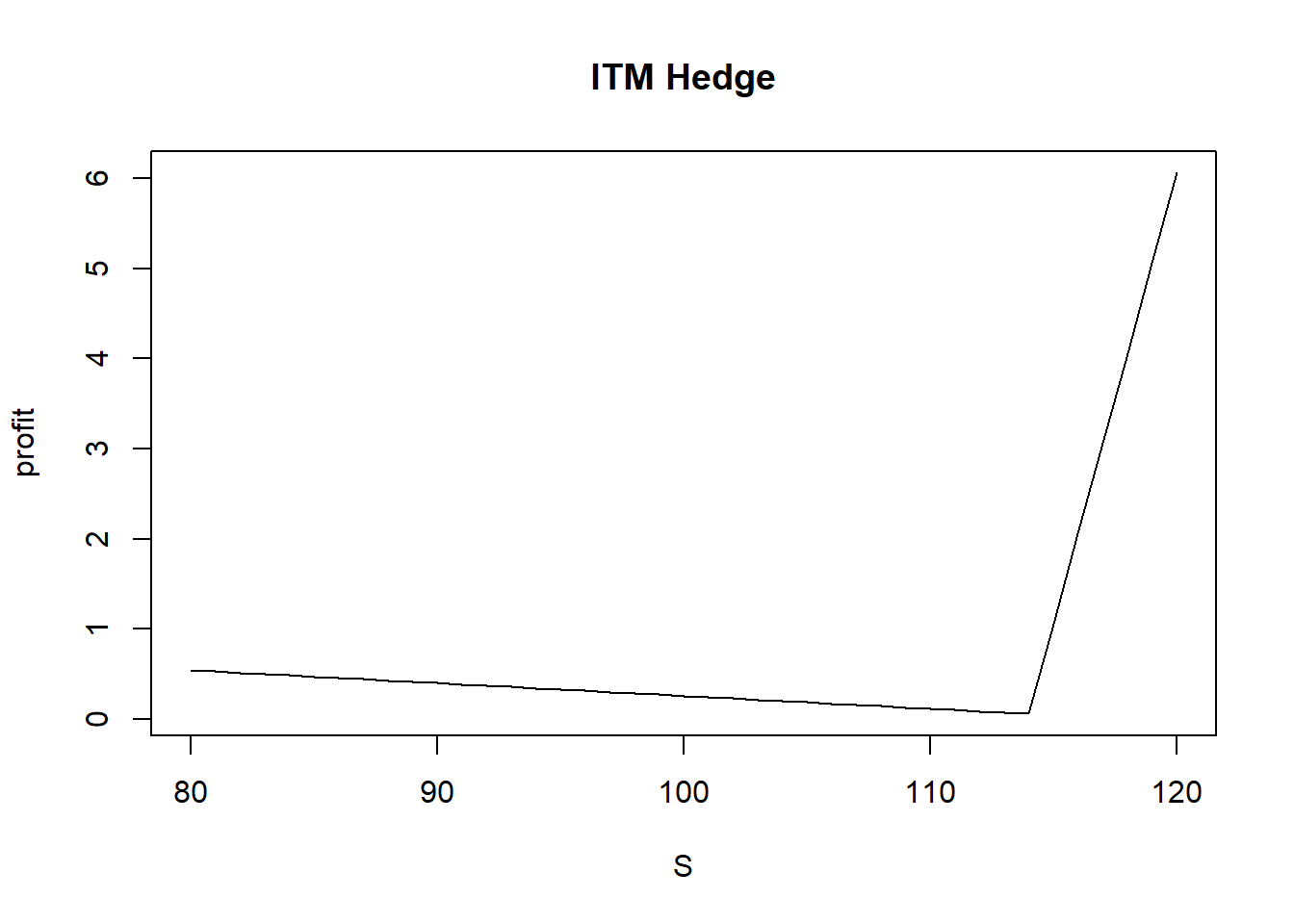
对冲收益一直为正，但是需要考虑流动性补偿和资金成本。

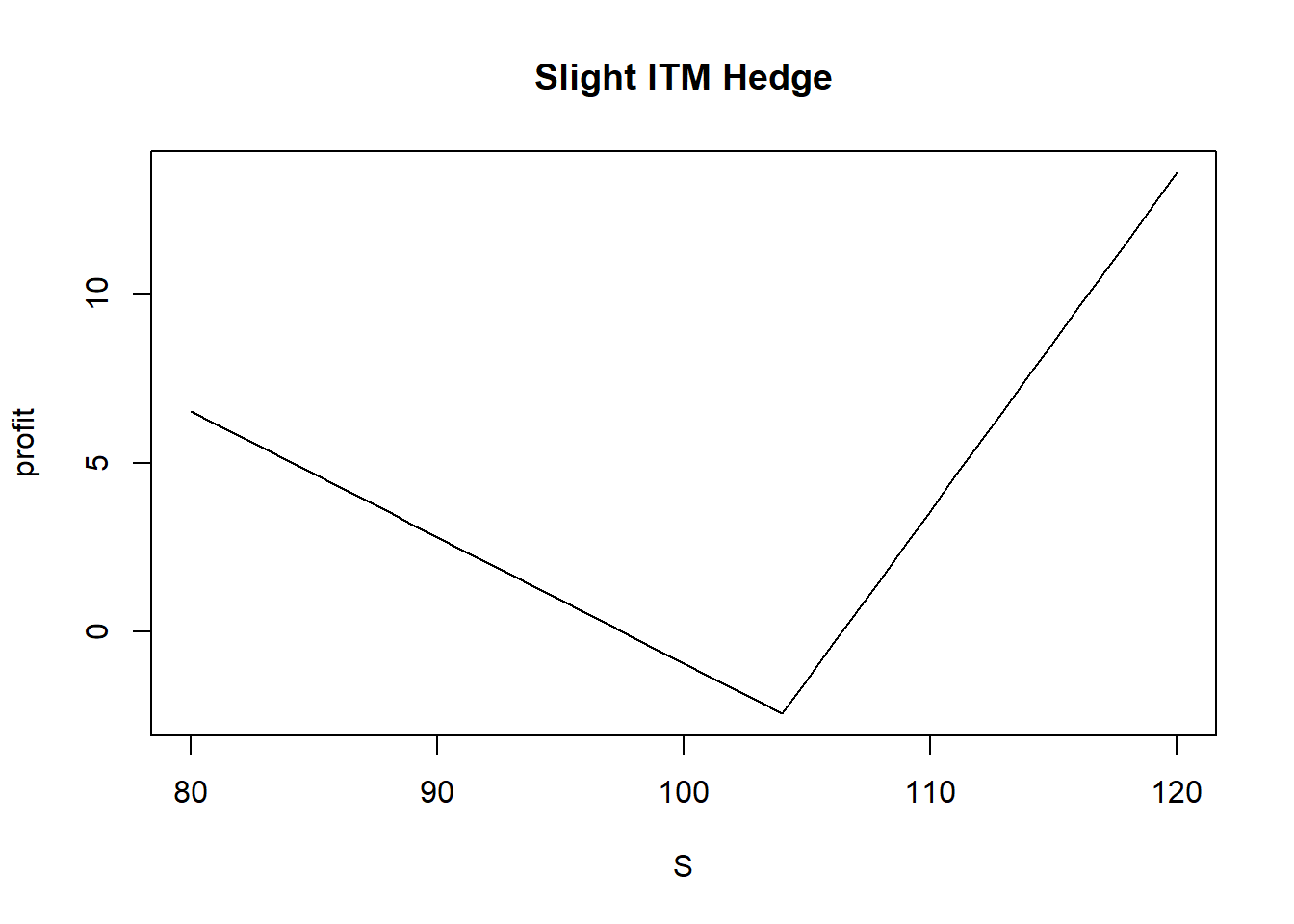
就是上面两种情况的综合了，需要承担一定的时间价值成本，但获利的空间比实值更大。

综上，在预计市场有大幅波动时，无论涨跌，选择平值期权进行Delta对冲。而震荡市且振幅较小时，在流动性补偿和资金占用均衡后，考虑采用较实值的合约对冲，或者采用一些贴水没那么严重的期货对冲。

其实，上述图形的变化，还是因为put端的Delta在变化，从而让组合在long Delta或者short Delta 和 long Gamma。

那是否需要定期调整Delta吗？

如果行情上涨，那Put的Delta变小，组合Delta变为正; 如果行情下跌，那组合Delta变为负，对组合Profit都是有利的。

定期调整Delta的话，那其实跟轻仓做买跨没啥区别，做的是波动率的上升。

Part2 合约面值对冲

先按合约面值对冲，k为对冲系数，\(k=I/K\)，始终只对冲一半。

1. 构建对冲价值变化

进入对冲时，价值变化量为 \[\Delta P=\Delta I + \frac{I}{K}\times \{max(K-I-\Delta I, 0) - \{max(K-I, 0) + T\}\}\]

2. 具体情况讨论

看起来很复杂，我们分情况讨论。

2.1 预测未来上涨

  1. 选择平值期权，K-I=0, \(k=1\) \[\frac{\Delta P}{P}=\frac{\Delta I - T}{I}\]

  2. 选择深度实值期权，\(k=0.5\)

  1. 上涨幅度没有超过实值程度，\(\Delta I < (K-I)\)

\[\frac{\Delta P}{P}= \frac{\Delta I-T}{2I}\]

  1. 上涨幅度超过实值程度，\(\Delta I > (K-I)\) \[\frac{\Delta P}{P}=\frac{\Delta I-I/K\times(K-I+T)}{I}\]

2.2 预测未来下跌

  1. 选择平值期权，K-I=0, \(k=1\) \[\frac{\Delta P}{P}=\frac{-T}{I}\]

  2. 选择深度实值期权，\(\Delta=1\)

\[\frac{\Delta P}{P}= \frac{\Delta I- T}{2I}\]

3. 一般性模拟和结论

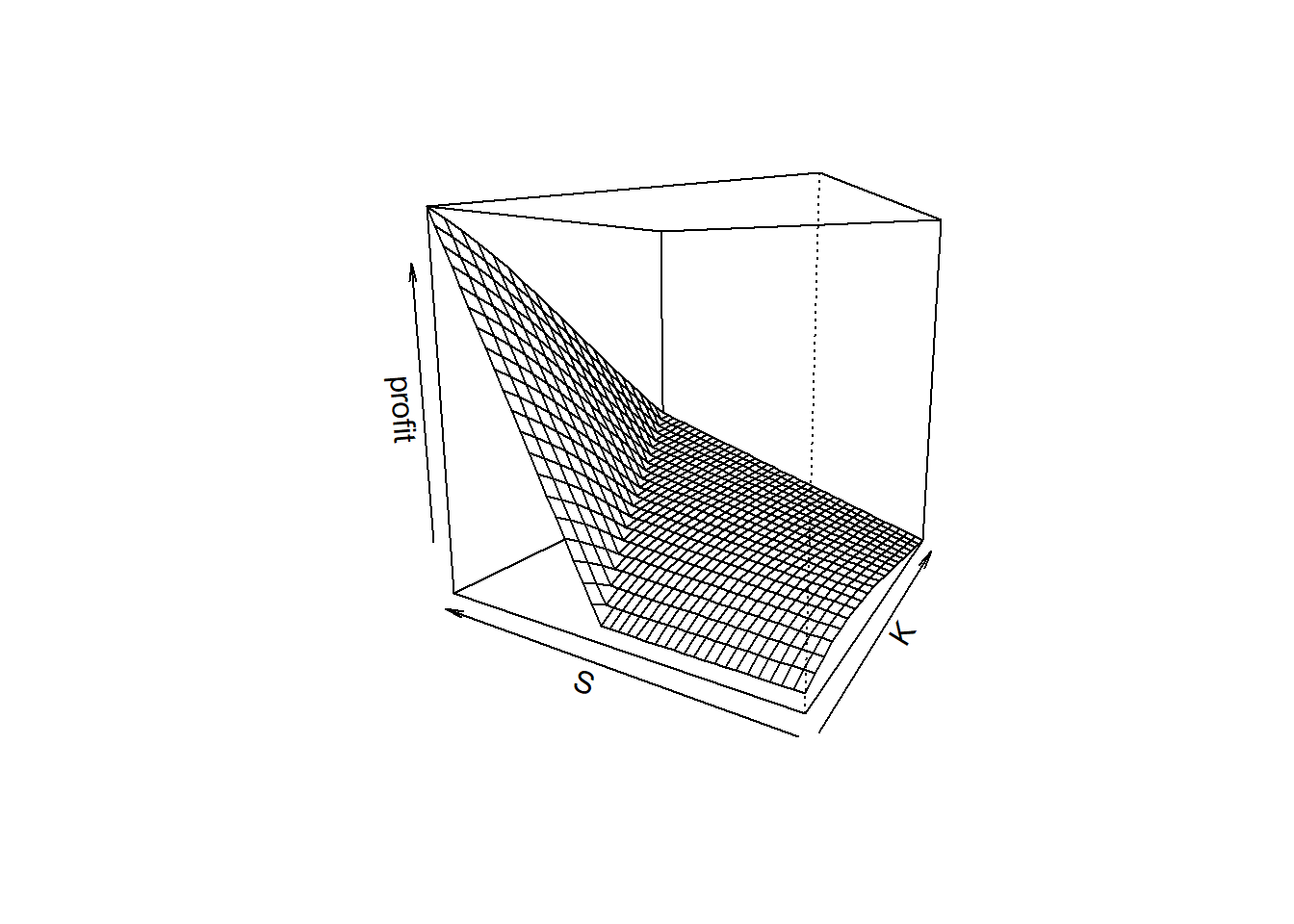
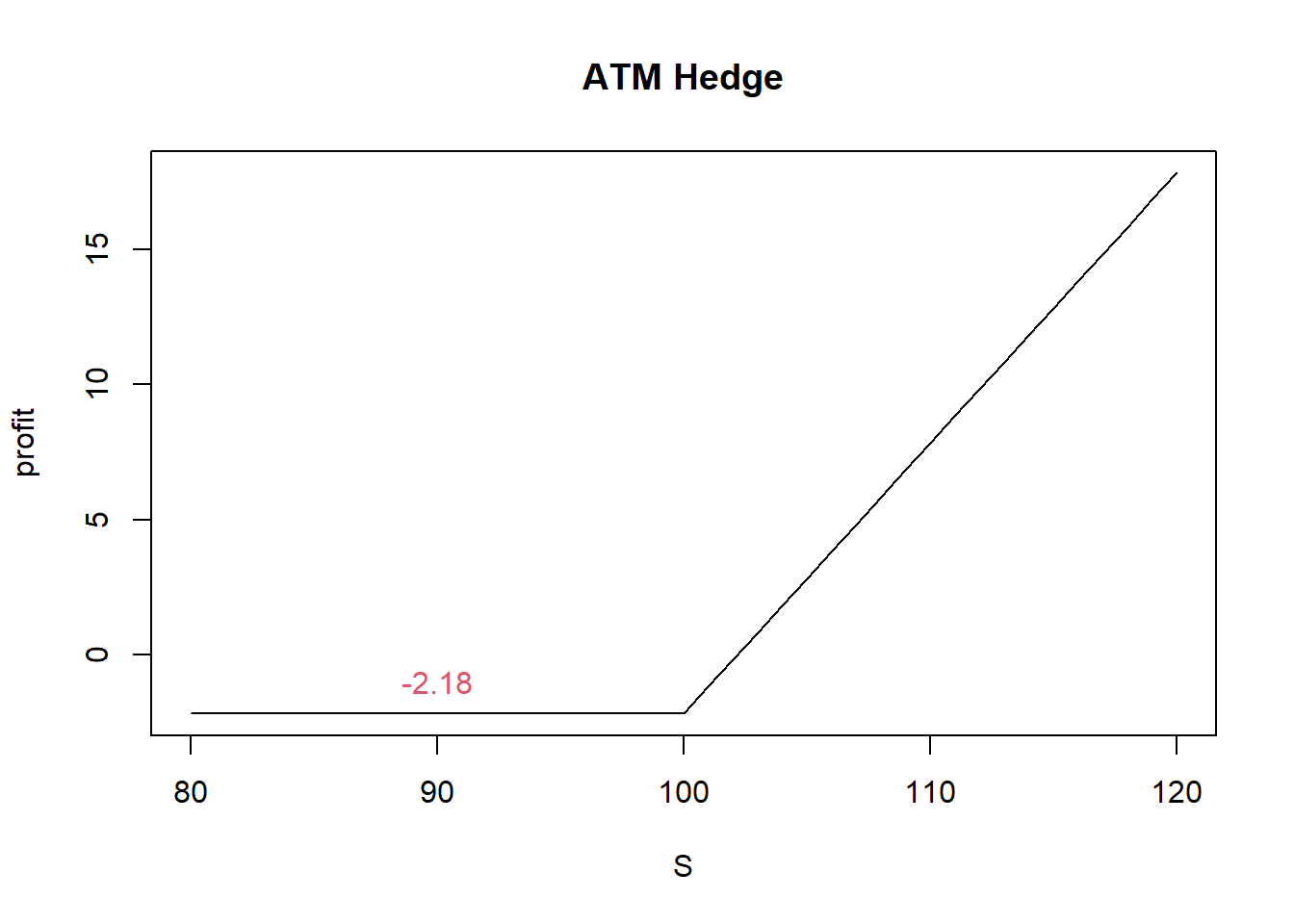对冲成本降低一半

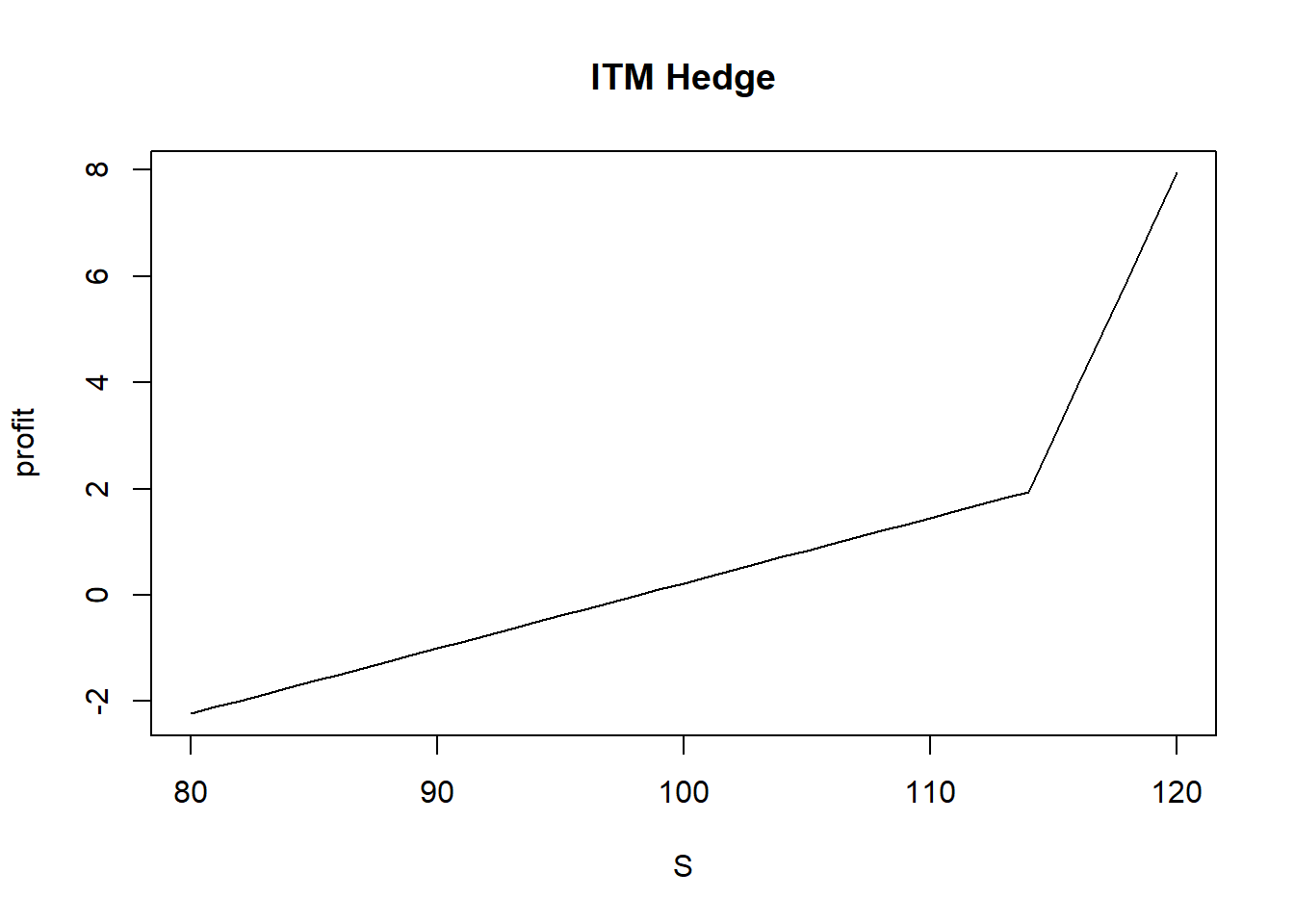
考虑流动性补偿和资金成本，可以考虑摈弃实值对冲了。

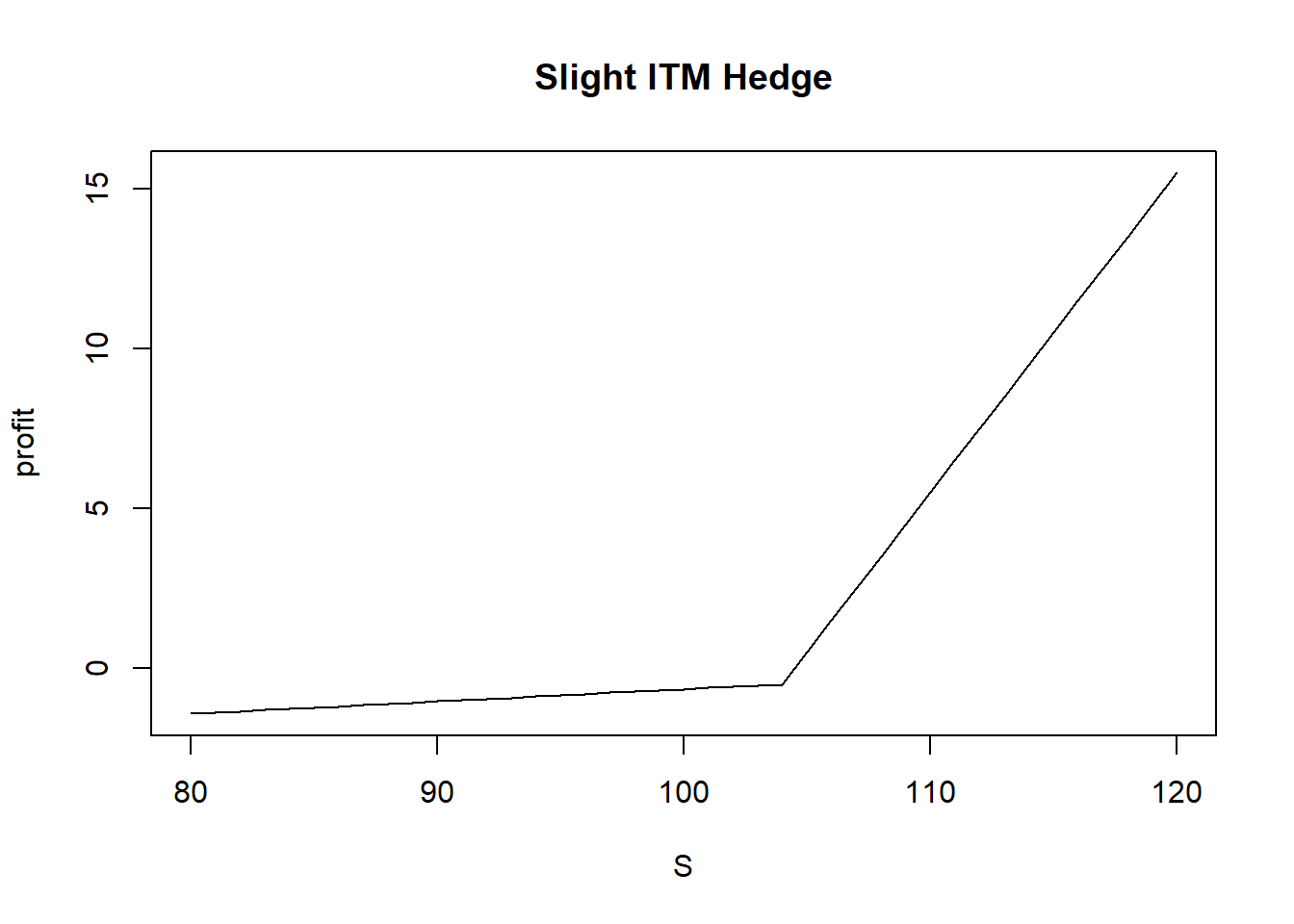
综上，其实按面值对冲成本更低，2.5%不到的成本（1个月）可以考虑在震荡市平价put对冲，相当于买个保险。如果Alpha收益差不多覆盖put成本，那基本上是无风险赚Beta的钱（大抵Alpha没那么高的收益，意思是这个意思）。

按面值对冲，本质就是hedge或者long delta 和 long Gamma。

Part3 结论

总结下来，建议还是按ATM来对冲，那按Delta还是面值来对冲？本质取决于你是否需要short Delta，也即以2.5%的成本来换取下跌时候的收益。 做Alpha的话，有必要short delta吗？